为庆祝“六一”儿童节，盐城市中小学统一组织文艺汇演，甲、乙两所学校共92人准备统一购买服装参加演出，其中甲校人数多于乙校人数，且甲校人数不够90 人。下面是某服装厂给出的演出服装的价格表：
| 购买服装的套数 |
1套至45套 |
46套至90套 |
91套及以上 |
| 每套服装的价格 |
60元 |
50元 |
40元 |
如果两所学校分别单独购买服装，一共应付5000元。
⑴如果甲、乙两校联合起来购买服装，那么比各自购买服装共可以节省多少钱？
⑵甲、乙两所学校各有多少名学生准备参加演出？
⑶如果甲校有10名同学抽调去参加书法绘画比赛而不能参加演出，请你为两所学校设计一种最省钱的购买服装方案。
已知：如图，△ABC内接于⊙O，点D在OC的延长线上，∠B=∠CAD=30°．
（1）求证：AD是⊙O的切线；
（2）若OD⊥AB，BC=4，求AD的长．
如图，点D、E分别为AB、AC边上两点，且AD=4，BD=" 2" ，AE=2，CE=10．
试说明：（1）△ADE∽△ACB ；（2）若BC=9，求DE的长．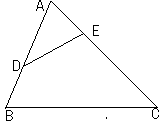
果农李明种植的草莓计划以每千克20元的单价对外批发销售，由于部分果农盲目扩大种植，造成该草莓滞销．李明为了加快 销售，减少损失，价格连续两次下调后，以每千克12.8元的单价对外批发销售．
（1）求李明平均每次下调的百分率；
（2）小刘准备到李明处购买2吨该草莓，因数量多，李明决定再给予两种优惠方案以供其选择：
方案一：在原下调后价格的基础上，再次以相同的百分率降价；
方案二：不打折，每吨优惠现金1800元．
试问小刘选择哪种方案更优惠，请说明理由．
如图，在由边长为1的小正方形组成的网格图中有△ABC，建立平面直角坐标系后，点O的坐标是（0，0）．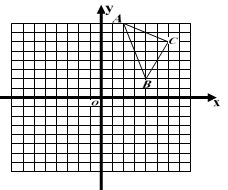
（1）以O为位似中心，作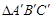
∽
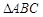，相似比为1：2，且保证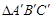在第三象限；
（2）点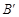
的坐标为（，）；
（3）若线段BC上有一点D，它的坐标为（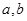
），那么它的对应点
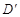的坐标为（，）．
已知关于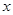
的方程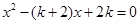
．
（1）试说明：无论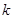
取什么实数值，方程总有实数根；
（2）若等腰△ABC的一边长a为1，另两边长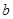
、c恰好是这个方程的两个实数根，求△ABC的周长．