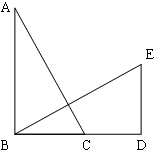
如图,点D、E分别为AB、AC边上两点,且AD=4,BD=" 2" ,AE=2,CE=10.
试说明:(1)△ADE∽△ACB ;(2)若BC=9,求DE的长.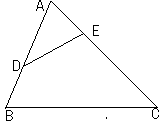
如图,在菱形 中,
中,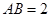 ,
, ,点
,点 是
是 边的中点,点
边的中点,点 是
是 边上一动点(不与点
边上一动点(不与点 重合),延长
重合),延长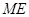 交射线
交射线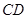 于点
于点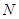 ,连接
,连接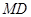 ,
,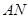 .
.
(1)求证:四边形 是平行四边形;
是平行四边形;
(2)填空:①当 的值为时,四边形
的值为时,四边形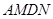 是矩形;
是矩形;
②当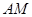 的值为时,四边形
的值为时,四边形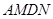 是菱形.
是菱形.
某校将举办“心怀感恩·孝敬父母”的活动,为此,校学生会就全校 名同学暑假期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成如下条形统计图.
名同学暑假期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成如下条形统计图.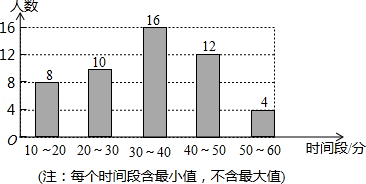
(1)填空:本次调查抽取的人数为_______,估计全校同学在暑假期间平均每天做家务活的时间在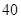 分钟以上(含
分钟以上(含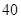 分钟)的人数为_______;
分钟)的人数为_______;
(2)校学生会拟在表现突出的甲、乙、丙、丁四名同学中,随机抽取两名同学向全校汇报.请用树状图或列表法表示出所有可能的结果,并求恰好抽到甲、乙两名同学的概率.
如图,定义:若双曲线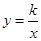
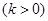 与它的其中一条对称轴y=x相交于A、B两点,则线段AB称为双曲线
与它的其中一条对称轴y=x相交于A、B两点,则线段AB称为双曲线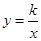
 的对径.
的对径.
(1)求双曲线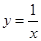 的对径的长;
的对径的长;
(2)若双曲线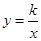
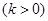 的对径的长是10
的对径的长是10 ,求k的值;
,求k的值;
(3)仿照上述定义,定义双曲线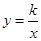
 的对径.
的对径.
如图,在 中,
中, ,点
,点 在
在 的延长线上,且
的延长线上,且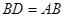 ,过
,过 作BE
作BE AC,与
AC,与 的垂线
的垂线 交于点
交于点 ,
,
(1)求证: ≌
≌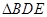 .
.
(2)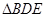 可由
可由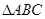 旋转得到,请用直尺和圆规作出旋转中心
旋转得到,请用直尺和圆规作出旋转中心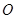 (保留作图痕迹,不写作法).
(保留作图痕迹,不写作法).
(1)计算: ;
;
(2)解方程组: