设函数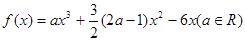
(1)当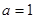 时,求曲线
时,求曲线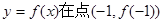 处的切线方程;
处的切线方程;
(2)当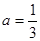 时,求
时,求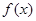 的极大值和极小值;
的极大值和极小值;
(3)若函数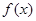 在区间
在区间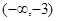 上是增函数,求实数
上是增函数,求实数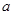 的取值范围.
的取值范围.
如图,△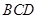 是等边三角形,
是等边三角形, 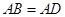 ,
,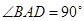 ,
,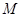 ,
,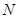 ,
,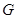 分别是
分别是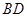 ,
,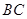 ,
,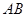 的中点,将△
的中点,将△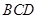 沿
沿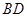 折叠到
折叠到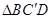 的位置,使得
的位置,使得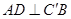 .
.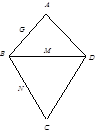
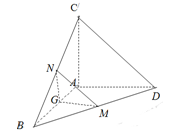
(1)求证:平面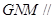 平面
平面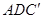 ;
;
(2)求证: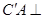 平面
平面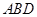 .
.
在直角坐标系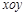 中,直线
中,直线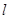 的参数方程为
的参数方程为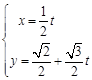 (
(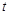 为参数),若以直角坐标系
为参数),若以直角坐标系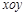 的
的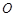 点为极点,
点为极点,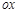 为极轴,且长度单位相同,建立极坐标系,得曲线
为极轴,且长度单位相同,建立极坐标系,得曲线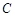 的极坐标方程为
的极坐标方程为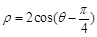 .
.
(1)求直线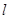 的倾斜角;
的倾斜角;
(2)若直线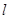 与曲线
与曲线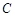 交于
交于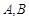 两点,求AB的距离.
两点,求AB的距离.
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:
性别与看营养说明列联表单位 名
| 男 |
女 |
总计 |
|
| 看营养说明 |
50 |
30 |
80 |
| 不看营养说明 |
10 |
20 |
30 |
| 总计 |
60 |
50 |
110 |
(1)从这50名女生中按是否看营养说明采取分层抽样,抽取一个容量为10的样本,问样本中看与不看营养说明的女生各有多少名?
(2)根据以上列联表,能否在犯错误的概率不超过0.01的前提下认为性别与是否看营养说明之间有关系?
下面的临界值表供参考:
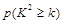 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
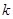 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: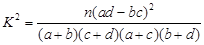 ,其中
,其中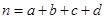 )
)
为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.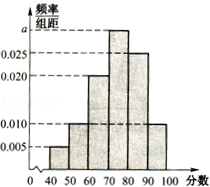
(1)若该校高三年级有1800人,试估计这次考试的数学成绩不低于60分的人数及60分以上的学生的平均分;
(2)若从[40,50)与[90,100]这两个分数段内的学生中随机选取两名学生,求这两名学生成绩之差的绝对值不大于10的概率
已知函数f(x)=xln(1+x)-a(x+1),其中a为实常数.
(1)当x∈[1,+∞)时,f′(x)>0恒成立,求a的取值范围;
(2)求函数g(x)=f′(x)-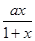 的单调区间.
的单调区间.