通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:
性别与看营养说明列联表 单位 名
| |
男 |
女 |
总计 |
| 看营养说明 |
50 |
30 |
80 |
| 不看营养说明 |
10 |
20 |
30 |
| 总计 |
60 |
50 |
110 |
(1)从这50名女生中按是否看营养说明采取分层抽样,抽取一个容量为10的样本,问样本中看与不看营养说明的女生各有多少名?
(2)根据以上列联表,能否在犯错误的概率不超过0.01的前提下认为性别与是否看营养说明之间有关系?
下面的临界值表供参考:
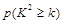 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
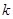 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: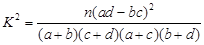 ,其中
,其中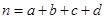 )
)
已知 是圆
是圆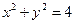 上满足条件
上满足条件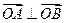 的两个点,其中
的两个点,其中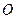 是坐标原点,分别过
是坐标原点,分别过 作
作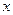 轴的垂线段,交椭圆
轴的垂线段,交椭圆 于
于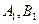 点,动点
点,动点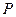 满足
满足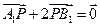
(I)求动点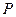 的轨迹方程.
的轨迹方程.
(II)设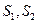 分别表示
分别表示 和
和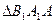 的面积,当点
的面积,当点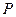 在
在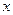 轴的上方,点
轴的上方,点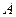 在
在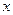 轴的下方时,求
轴的下方时,求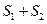 的最大面积.
的最大面积.
如图,正方形 所在平面与圆
所在平面与圆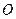 所在平面相交于
所在平面相交于 ,线段
,线段 为圆
为圆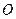 的弦,
的弦,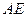 垂直于圆
垂直于圆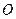 所在平面,垂足
所在平面,垂足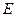 是圆
是圆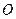 上异于
上异于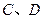 的点,
的点, ,圆
,圆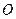 的直径为
的直径为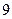 ,
,
1)求证:平面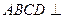 平面
平面 2)求二面角
2)求二面角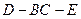 的平面角的正切值.
的平面角的正切值.
若抛物线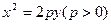 的焦点与椭圆
的焦点与椭圆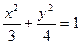 的上焦点重合,
的上焦点重合,
1)求抛物线方程.
2)若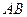 是过抛物线焦点的动弦,直线
是过抛物线焦点的动弦,直线 是抛物线两条分别切于
是抛物线两条分别切于 的切线,求
的切线,求 的交点的纵坐标.
的交点的纵坐标.
如图,四棱锥 中,底面
中,底面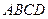 是矩形,
是矩形,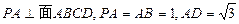 ,点
,点 是
是 的中点,点
的中点,点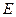 在边
在边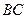 上移动。
上移动。
1)点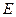 为
为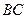 的中点时,试判断
的中点时,试判断 与平面
与平面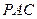 的位置关系,并说明理由。
的位置关系,并说明理由。
2)证明:无论点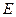 在边
在边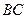 的何处,都有
的何处,都有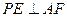
3)当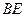 等于何值时,
等于何值时,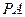 与平面
与平面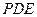 所成角的大小为
所成角的大小为 .
.
已知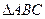 的两个顶点
的两个顶点 的坐标分别
的坐标分别 ,且
,且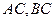 所在直线的斜率之积为
所在直线的斜率之积为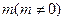 ,1)求顶点
,1)求顶点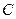 的轨迹.2)当
的轨迹.2)当 时,记顶点
时,记顶点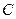 的轨迹为
的轨迹为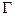 ,过点
,过点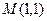 能否存在一条直线
能否存在一条直线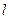 ,使
,使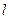 与曲线
与曲线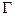 交于
交于 两点,且
两点,且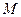 为线段
为线段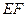 的中点,若存在求直线
的中点,若存在求直线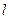 的方程,若不存在说明理由.
的方程,若不存在说明理由.