已知函数 (x≠0),各项均为正数的数列
(x≠0),各项均为正数的数列 中
中 ,
, ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)在数列 中,对任意的正整数
中,对任意的正整数 ,
,  都成立,设
都成立,设 为数列
为数列 的前
的前 项和试比较
项和试比较 与
与 的大小.
的大小.
(本小题14分)已知直线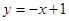 与椭圆
与椭圆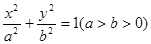 相交于A、B两点,
相交于A、B两点,
且线段AB的中点在直线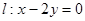 上.
上.
(1)求此椭圆的离心率;
(2)若椭圆的右焦点关于直线 的对称点的在圆
的对称点的在圆 上,求此椭圆的方程.
上,求此椭圆的方程.
(本小题满分13分)
如图,在四棱锥 中,底面
中,底面 四边长为1的菱形,
四边长为1的菱形, ,
,  ,
,  ,
, 为
为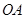 的中点,
的中点, 为
为 的中点
的中点
(Ⅰ)证明:直线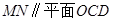
 ;
;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离。
(本小题满分12分)
命题p:实数x满足x2-4ax+3a2<0,其中a<0,命题q:实数x满足x2-x-6≤0,且q是p的必要不充分条件,求a的取值范围.
( 本小题满分12分)
在数列 中,
中,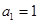 ,
, .
.
(Ⅰ)设 .证明:数列
.证明:数列 是等差数列;
是等差数列;
(Ⅱ)求数列 的前
的前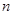 项和
项和 .
.
(本小题满分12分)
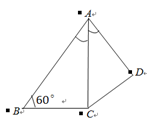
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=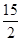 ,求AB的长.
,求AB的长.