连接上海市区到浦东国际机场的磁悬浮轨道全长约为
，列车走完全程包含启动加速、匀速运行、制动减速三个阶段．已知磁悬浮列车从启动加速到稳定匀速动行共需
秒，在这段时间内记录下下列数据：
时间 （秒） |
0 |
50 |
100 |
150 |
200 |
速度 （米／秒） |
0 |
30 |
60 |
90 |
120 |
路程 （米） |
0 |
750 |
3000 |
6750 |
12000 |
请你在一次函数、二次函数和反比例函数中选择合适的函数来分别表示在加速阶段（
）速度与时间的函数关系、路程
与时间的函数关系最新研究表明，此种列车的稳定动行速度可达180米／秒，为了检测稳定运行时各项指标，在列车达到这一速度后至少要运行100秒，才能收集全相关数据．若在加速过程中路程、速度随时间的变化关系仍然满足（1）中的函数关系式，并且制作减速所需路程与启动加速的路程相同．根据以上要求，至少还要再建多长轨道就能满足试验检测要求？
若减速过程与加速过程完全相反．根据对问题（2）的研究，直接写出列车在试验检测过程中从启动到停车这段时间内，列车离开起点的距离
（米）与时间（秒）的函数关系式（不需要写出过程）
为了把一个长100m宽60m的游泳池扩建成一个周长为600m的大型水上游乐场，把游泳池的长增加xm，那么x等于多少时，水上游乐场的面积为20000㎡？如果能，求出x的值；如果不能，请说明理由。
如图，以平行四边形ABCD的顶点A为圆心，AB为半径作圆交AD，BC于点E，F，延长BA交⊙Ｏ于G。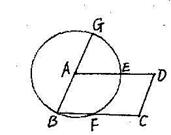
求证：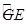
＝
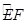
如图，点O、B坐标分别为（0，0）（3，0），将△OAB绕O点逆时针方向旋转90°到△A1B1O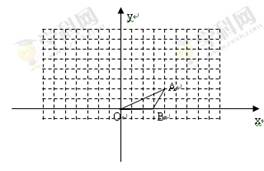
（1）画出△A1B1O；
（2）写出A1点的坐标；
（3）求出BB1的长.
关于x的一元二次方程x2+3x+m﹣1=0的两个实数根分别为x1，x2．
（1）求m的取值范围；
（2）若2（x1+x2）+x1x2+10=0，求m的值．
已知
，化简求值：