已知数列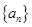 中,
中,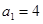 ,
,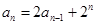 (
(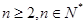 ).
).
(Ⅰ)求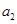 和
和 的值;
的值;
(Ⅱ)求数列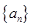 的通项公式.
的通项公式.
(本小题满分10分)
(1)计算:C +C
+C +C
+C +…+C
+…+C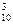 (2)证明:A
(2)证明:A +kA
+kA =A
=A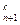
(本小题12分)设函数f(x)=a·b,其中a=(2cosx,1), b=(cosx, sin2x), x∈R.
sin2x), x∈R.
(1)若f(x)=1- ,且x∈[
,且x∈[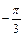 ,
,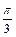 ],求x;
],求x;
(2)若函数y=2sin2x的图象按向量c=(m,n)(|m|<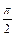 )平移后得到函数y= f(x)的图象,求实数m、n的值.
)平移后得到函数y= f(x)的图象,求实数m、n的值.
(本小题10分) 已知函数 在其一个周期内的图象上有一个最高点
在其一个周期内的图象上有一个最高点 和一个最低点
和一个最低点 。
。
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求 的单调增区间。
的单调增区间。
(本小题10分)已知 ,且
,且 .
.
(Ⅰ)求 、
、 的值;
的值;
(Ⅱ)求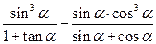 的值.
的值.
(本小题10分) 已知 ,
, ,当
,当 为何值时,
为何值时,
(Ⅰ)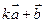 与
与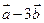 垂直?
垂直?
(Ⅱ) 与
与 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?