如图, 为多面体,平面
为多面体,平面 与平面
与平面 垂直,点
垂直,点 在线段
在线段 上,
上, △OAB,,△
△OAB,,△ ,△
,△ ,△
,△ 都是正三角形。
都是正三角形。
(Ⅰ)证明直线 ∥
∥ ;
;
(II)求棱锥F—OBED的体积。
:如图,在三棱锥 中,
中,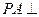 底面ABC,
底面ABC,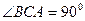 ,AP="AC," 点
,AP="AC," 点 ,
,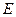 分别在棱
分别在棱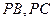 上,且BC//平面ADE
上,且BC//平面ADE
(Ⅰ)求证:DE⊥平面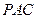 ;
; (Ⅱ)当二面角
(Ⅱ)当二面角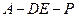 为直二面角时,求多面体ABCED与PAED的体积比。
为直二面角时,求多面体ABCED与PAED的体积比。
:已知函数 。
。
(Ⅰ)求 的值域;
的值域;
(Ⅱ)若 (x>0)的图象与直线
(x>0)的图象与直线 交点的横坐标由小到大依次是
交点的横坐标由小到大依次是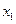 ,
,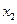 ,…,
,…,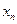 ,求数列
,求数列 的前
的前 项的和。
项的和。
(14分)
定义:若函数 对于其定义域内的某一数
对于其定义域内的某一数 ,有
,有 ,则称
,则称 是
是 的一个不动点. 已知函数
的一个不动点. 已知函数 .
.
(1)当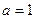 ,
, 时,求函数
时,求函数 的不动点;
的不动点;
(2)若对任意的实数b,函数 恒有两个不动点,求a的取值范围;
恒有两个不动点,求a的取值范围;
(3)在(2)的条件下,若
 图象上两个点A、B的横坐标是函数
图象上两个点A、B的横坐标是函数 的不动点,且A、B的中点C在函数
的不动点,且A、B的中点C在函数 的图象上,求b的最小值.
的图象上,求b的最小值.
(参考公式: 的中点坐标为
的中点坐标为 )
)
(14分) 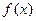 是定义在R上的函数,对
是定义在R上的函数,对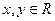 都有
都有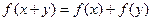 ,且当
,且当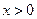 时,
时,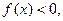
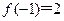 。
。
(1)求证: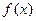 为奇函数;
为奇函数;
(2)求证: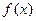 是R上的减函数;
是R上的减函数;
(3)求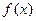 在
在 上的最值。
上的最值。
( 14分)
已知函数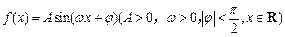 的部分图象如图2所示,
的部分图象如图2所示,
(1)求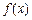 的解析式;
的解析式;
(2)求直线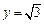 与函数
与函数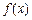 图象的所有交点的坐标.
图象的所有交点的坐标.