如图,直角三角形 的顶点坐标
的顶点坐标 ,直角顶点
,直角顶点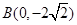 ,顶点
,顶点 在
在 轴上,点
轴上,点 为线段
为线段 的中点
的中点
(Ⅰ)求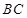 边所在直线方程;
边所在直线方程;
(Ⅱ)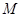 为直角三角形
为直角三角形 外接圆的圆心,求圆
外接圆的圆心,求圆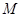 的方程;
的方程;
(Ⅲ)若动圆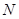 过点
过点 且与圆
且与圆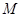 内切,求动圆
内切,求动圆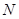 的圆心
的圆心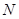 的轨迹方程.
的轨迹方程.
宇宙深处有一颗美丽的行星,这个行星是一个半径为r(r>0)的球。人们在行星表面建立了与地球表面同样的经纬度系统。已知行星表面上的A点落在北纬60°,东经30°;B点落在东经30°的赤道上;C点落在北纬60°,东经90°。在赤道上有点P满足PB两点间的球面距离等于AB两点间的球面距离。
(1)求AC两点间的球面距离;
(2)求P点的经度;
(3)求AP两点间的球面距离。
设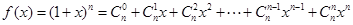 (
(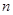 是正整数),利用赋值法解决下列问题:
是正整数),利用赋值法解决下列问题:
(1)求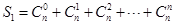 ;
;
(2)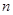 为偶数时,求
为偶数时,求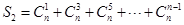 ;
;
(3)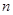 是3的倍数时,求
是3的倍数时,求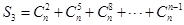 。
。
已知:对于任意的多项式 与任意复数z,
与任意复数z,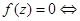
 整除
整除 。利用上述定理解决下列问题:
。利用上述定理解决下列问题:
在复数范围内分解因式: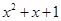 ;
;
求所有满足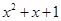 整除
整除 的正整数n构成的集合A。
的正整数n构成的集合A。
如图,已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点。
(1)求证:直线AB1∥平面C1DB;
(2)求异面直线AB1与BC1所成角的余弦值
如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线。
(1)求证:OB⊥AC;
(2)若AC与圆柱下底面所成的角为30°,OA=2。求三棱锥A-BOC的体积。