某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:
设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?
(成本=进价×销售量)
如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC.
(1)求证:AB是⊙O的切线;
(2)若PC=2 ,OA=3,求⊙O的半径.
,OA=3,求⊙O的半径.
父亲节快到了,明明准备为爸爸煮四个大汤圆作早点:一个芝麻馅,一个水果馅,两个花生馅,四个汤圆除内部馅料不同外,其它一切均相同(分别用A,B,C表示芝麻馅、水果馅、花生馅的大汤圆)。
(1)求爸爸吃前两个汤圆刚好都是花生馅的概率;
(2)若给爸爸再增加一个花生馅的汤圆,则爸爸吃前两个汤圆都是花生的可能性是否会增大?请说明理由.
如图,抛物线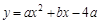 的对称轴为直线x=
的对称轴为直线x=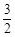 ,与
,与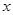 轴交于A,B两点,与y轴交于点C(0,4)
轴交于A,B两点,与y轴交于点C(0,4)
(1)求抛物线的解析式,结合图象直接写出当0≤x≤4时y的取值范围;
(2)已知点D(m,m+1)在第一象限的抛物线上,点D关于直线BC的对称点为点E,求点E的坐标.
画图:在平面直角坐标系中, 的位置如图所示,且点A(-3,4),B(0,3)
的位置如图所示,且点A(-3,4),B(0,3)
|
 绕点O顺时针旋转90°后得到的
绕点O顺时针旋转90°后得到的 ;
;
 ,
, 的坐标;
的坐标;
电动自行车已成为市民日常出行的首选工具。据某市品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月销售216辆。
(1)求该品牌电动车销售量的月平均增长率;
(2)若该品牌电动自行车的进价为2300元,售价2800元,则该经销商1月至3月共盈利多少元?