如图，用一根长为18米的篱笆靠墙围成一个长方形的空地用于绿化，且平行墙的一边为长，墙的长为12米。
（1）若长方形的长比宽多1.5米,此时长、宽各是多少米？
（2）在与墙平行的一边开设一个宽为1米的门（用其它材料），使长方形的长比宽多4米，此时它所围成的长方形的面积是多少米2？
（3）若每块长方形草皮长1米、宽0.5米,每块草皮30元，铺满整块绿化地所购买的草皮不超过2400元，请试探究符合条件的长方形的长和宽的长度（长＞宽且长、宽取整数）？
定义一种新运算“⊕”：a⊕b=a-2b，比如：2⊕（-3）=2-2×（-3）=2+6=8．
（1）求（-3）⊕2的值；
（2）若（x-3）⊕（x+1）=1，求x的值．
已知一次函数y=
x+3的图象与x轴、y轴分别交于A、B两点，以线段AB为直角边在第二象限内左等腰直角三角形ABC，∠BAC=90°，如图1所示．
（1）填空：AB= ，BC= ．
（2）将△ABC绕点B逆时针旋转，
①当AC与x轴平行时，则点A的坐标是
②当旋转角为90°时，得到△BDE，如图2所示，求过B、D两点直线的函数关系式．
③在②的条件下，旋转过程中AC扫过的图形的面积是多少？
（3）将△ABC向右平移到△A′B′C′的位置，点C′为直线AB上的一点，请直接写出△ABC扫过的图形的面积．
为了解甲、乙两种车的刹车距离，经试验发现，甲车的刹车距离s甲是车速v的
，乙车的刹车距离s乙等于反应距离与制动距离之和，二反应距离与车速v成正比，制动距离与车速v2成正比，具体关系如下表：
| 车速v（km/h） |
40 |
50 |
| 刹车距离s乙（m） |
12 |
17.5 |
（1）分别求出s甲、s乙与车速v的函数关系式；
（2）若乙车在限速120km/h的高速公路上行驶，乙车的最长刹车距离是多少m？
（3）刹车速度是处理交通事故的一个重要因素，请看下面一个交通事故案例：甲、乙两车在限速为80km/g的道路上相向而行，等望见对方，同时刹车时已晚，两车还是相撞了，事后经现场勘查，测得甲车的刹车距离超过16m，但小于18m，乙车的刹车距离是24m，请你比较两车的速度，并判断哪辆车超速？
如图1，AB是⊙O的直径，点C在⊙O上，且点C为弧BE的中点，连接AE并延长交BC延长线于点D．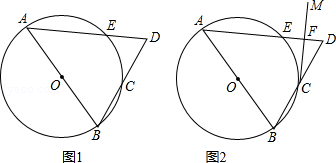
（1）判断△ABD的形状，并说明理由；
（2）过点C作CM⊥AD，垂足为点F，如图2．
①求证：CF是⊙O的切线；
②若⊙O的半径为3，DF=1，求sinB的值．
问题发现：
如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．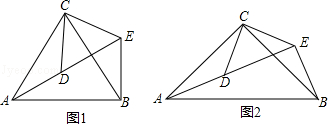
（1）求证：△ACD≌△BCE；
（2）求证：CD∥BE．
拓展探究：
如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，连接BE，求∠AEB的度数．