如图，四边形ABCD为矩形，AB＝4，AD＝3，动点M、N分别从D、B同时出发，以1个单位/秒的速度运动，点M沿DA向终点A运动，点N沿BC向终点C运动。过点N作NP⊥BC，交AC于点P，连结MP。已知动点运动了
秒。
请直接写出PN的长 ；（用含
的代数式表示）若0秒≤
≤3秒，试求△MPA的面积S与时间秒的函数关系式，并求S的最大值。若0秒≤
≤3秒，△MPA能否与△PCN相似？若能，试求出相似时的对应值；若不能，试说明理由。
在梯形ABCD中，AD∥BC，AC⊥BD，若AD=2，BC=8，BD=6，
求：（1）对角线AC的长；（2）梯形ABCD的面积.
如图，在梯形ABCD中，AB∥CD，AD=BC，延长AB到E，使BE=DC，连结AC、CE，你能用几种方法说明AC与CE相等？请你写出一种推理过程.
如图，在梯形ABCD中，AB∥CD，M、N分别为CD、AB中点，且MN⊥AB.梯形ABCD一定为等腰梯形，请你用两种不同的方法说明理由.
在梯形ABCD中，AB∥CD，∠A=∠B，E是AB中点，EC等于ED吗？为什么？
如图，△ABC中，点O是AC边上一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于E，交∠BCA的外角平分线于点F.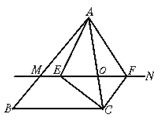
(1)求证：EO=FO
(2)当点O运动到何处时，四边形AECF是矩形？并证明你的结论.