现有6本不同的书,按下列要求各有多少种不同的分法:
(I)分为三份,每份2本;
(II)分给甲、乙、丙三人每人2本;
(III)分给甲、乙、丙三人;
(IV)分给甲、乙、丙三人,每人至少1本.
(最后结果请用数字表示).
(选修4—2:矩阵与变换)
设矩阵 的一个特征值为
的一个特征值为 ,若曲线
,若曲线 在矩阵
在矩阵 变换下的方程为
变换下的方程为 ,求曲线
,求曲线 的方程.
的方程.
(选修4—1:几何证明选讲)
如图, 为⊙
为⊙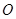 的直径,直线
的直径,直线 与⊙
与⊙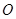 相切于点
相切于点 ,
,
 ,
,
 ,
,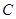 、
、 为垂足,连接
为垂足,连接 . 若
. 若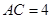 ,
,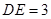 ,求
,求 的长.
的长.
设数列 共有
共有 项,记该数列前
项,记该数列前 项
项 中的最大项为
中的最大项为 ,该数列后
,该数列后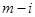 项
项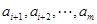 中的最小项为
中的最小项为 ,
, .
.
(1)若数列 的通项公式为
的通项公式为 ,求数列
,求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,
, ,求数列
,求数列 的通项公式;
的通项公式;
(3)试构造一个数列 ,满足
,满足 ,其中
,其中 是公差不为零的等差数列,
是公差不为零的等差数列,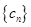 是等比数列,使得对于任意给定的正整数
是等比数列,使得对于任意给定的正整数 ,数列
,数列 都是单调递增的,并说明理由.
都是单调递增的,并说明理由.
已知函数 在
在 处的切线方程为
处的切线方程为 .
.
(1)求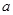 的值;
的值;
(2)若对任意的 ,都有
,都有 成立,求
成立,求 的取值范围;
的取值范围;
(3)若函数 的两个零点为
的两个零点为 ,试判断
,试判断 的正负,并说明理由.
的正负,并说明理由.
如图,在平面直角坐标系 中,设点
中,设点 是椭圆
是椭圆 上一点,从原点
上一点,从原点 向圆
向圆 作两条切线分别与椭圆
作两条切线分别与椭圆 交于点
交于点 ,直线
,直线 的斜率分别记为
的斜率分别记为 .
.
(1)若圆 与
与 轴相切于椭圆
轴相切于椭圆 的右焦点,求圆
的右焦点,求圆 的方程;
的方程;
(2)若 .
.
①求证: ;
;
②求 的最大值
的最大值