高考数学考试中共有10道选择题,每道选择题都有4个选项，其中有且仅有一个是正确的.评分标准规定：“在每小题给出的四个选项中，只有一项是符合题目要求的，答对得5分，不答或答错得0分”.某考生每道选择题都选出了一个答案，能确定其中有6道题的答案是正确的，而其余题中，有两道题都可判断出有两个选项是错误的，有一道题可以判断一个选项是错误的，还有一道题因不理解题意只能乱猜.
试求出该考生的选择题：
（I）得30分的概率；
（II）得多少分的概率最大；
（III）所得分数
的数学期望．
(本小题满分14分)如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD
所在的平面和圆O所在的平面互相垂直，且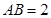
，
.
(1)求证：
平面
；
(2)设FC的中点为M，求证：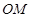
∥平面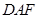
；
(3)求三棱锥F－CBE的体积.
(本小题满分14分)
已知向量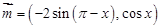
，
，函数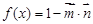
．
(1)求函数
的解析式；
(2)当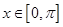
时，求的单调递增区间；
(3)说明的图象可以由
的图象经过怎样的变换而得到．
．(本小题满分12分)
已知集合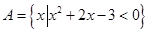
，
，
(1)在区间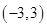
上任取一个实数
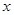，求“
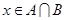”的概率；
(2)设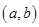
为有序实数对，其中
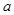是从集合
中任取的一个整数，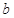
是从集合
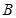中任取的一个整数，求“
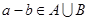”的概率.
、(本小题满分14分)设函数
(Ⅰ)求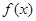
的单调区间；
(Ⅱ)当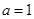
时，若方程
在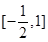
上有两个实数解，求实数t的取值范围；
(Ⅲ)证明：当m>n>0时，
(本小题满分14分) 已知数列
满足：
(Ⅰ)探究数列
是等差数列还是等比数列，并由此求数列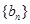
的通项公式；
(Ⅱ)求数列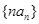
的前n项和