如图9, 已知抛物线与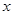 轴交于A (-4,0) 和B(1,0)两点,与
轴交于A (-4,0) 和B(1,0)两点,与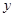 轴交于C(0,-2)点.
轴交于C(0,-2)点.求此抛物线的解析式;
设G是线段BC上的动点,作GH//AC交AB于H,连接CF,当△BGH的面积是△CGH面积的3倍时,求H点的坐标;
若M为抛物线上A、C两点间的一个动点,过M作
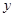 轴的平行线,交AC于N,当M点运动到什么位置时,线段MN的值最大,并求此时M点的坐标
轴的平行线,交AC于N,当M点运动到什么位置时,线段MN的值最大,并求此时M点的坐标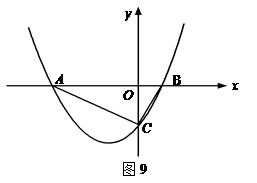
已知:如图,在△ABC中,∠ACB=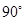 ,过点C作CD⊥AB于点D,点E为AC上一点,过E点作AC的垂线,交CD的延长线于点F ,与AB交于点G.求证:△ABC∽△FGD
,过点C作CD⊥AB于点D,点E为AC上一点,过E点作AC的垂线,交CD的延长线于点F ,与AB交于点G.求证:△ABC∽△FGD
计算: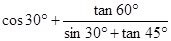
在△ABC中,AB、BC、AC三边的长分别为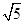 、
、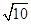 、
、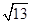 ,求这个三角形的面积.
,求这个三角形的面积.
小华同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样就不需要求△ABC的高,而借用网格就能计算出它的面积.(本题8分)
⑴ 请你将△ABC的面积直接填写在横线上.
思维拓展:
⑵ 我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为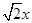 、
、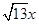 、
、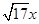 (
(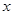 >0),请利用图②的正方形网格(每个小正方形的边长为
>0),请利用图②的正方形网格(每个小正方形的边长为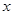 )画出相应的△ABC,并求出它的面积.
)画出相应的△ABC,并求出它的面积.
探索创新:
⑶ 若△ABC三边的长分别为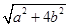 、
、 、
、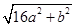 (
(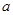 >0,
>0,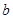 >0,且
>0,且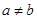 ),试运用构图法求出这个三角形的面积.
),试运用构图法求出这个三角形的面积.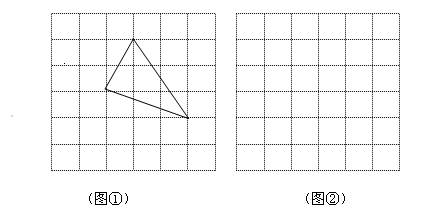
图1,两个不全等的等腰直角三角形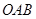 和
和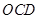 叠放在一起,并且有公共的直角顶点
叠放在一起,并且有公共的直角顶点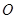 .
.
⑴在图1中,你发现线段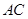 ,
,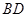 的数量关系是,直线
的数量关系是,直线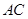 ,
,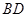 相交成度角.
相交成度角.
⑵将图1中的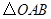 绕点
绕点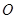 顺时针旋转
顺时针旋转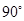 角,得到图2,这时(1)中的两个结论是否成立?请做出判断并说明理由.
角,得到图2,这时(1)中的两个结论是否成立?请做出判断并说明理由.
⑶将图1中的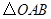 绕点
绕点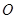 顺时针旋转一个锐角,得到图3,这时(1)中的两个结论是否成立?(请直接回答结论)
顺时针旋转一个锐角,得到图3,这时(1)中的两个结论是否成立?(请直接回答结论)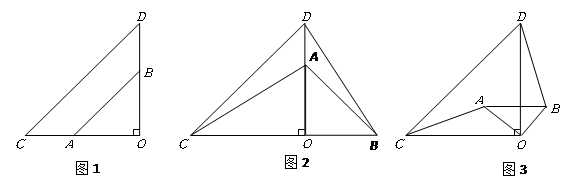
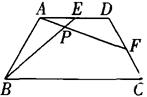
如图,在等腰梯形ABCD中,AD∥BC,∠C=60°,AD=CD.E、F分别在AD、CD上,DE=CF,AF、BE交于点P.
⑴试说明:AF=BE⑵猜测∠BPF的度数,并说明你的结论的正确性.