设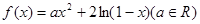 ,
,
(1)若 在
在 处有极值,求a;
处有极值,求a;
(2)若 在
在 上为增函数,求a的取值范围.
上为增函数,求a的取值范围.
( 本题满分15分)
本题满分15分)
已知偶函 数
数 满足:当
满足:当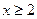 时,
时,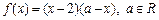 ,当
,当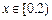 时,
时,
(1) 求当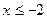 时,
时,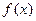 的表达式;
的表达式;
(2) 若直线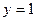 与函数
与函数 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数 的取值范围。
的取值范围。 (3) 试讨论当实数
(3) 试讨论当实数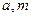 满足什么条件时,函数
满足什么条件时,函数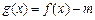 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。
(本题满分15分)已知函数
(1) 求函数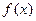 的最小值
的最小值
(2)求证:当 时
时 ,
,
(本题满分14分)
已知函数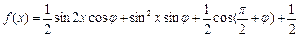 ,
,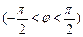 ,其图象过点
,其图象过点
(1) 求 的解析式,并求对称中心
的解析式,并求对称中心
(2) 将函数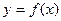 的图象上各点纵坐标不变,横坐标扩大为原来的2倍,然后各点横坐标不变,纵坐标扩大为原来的2倍,得到
的图象上各点纵坐标不变,横坐标扩大为原来的2倍,然后各点横坐标不变,纵坐标扩大为原来的2倍,得到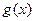 的图象,求函数
的图象,求函数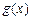 在
在 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)
设双曲线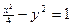 的右顶点为
的右顶点为 是双曲线上异于顶点的一个动点,从
是双曲线上异于顶点的一个动点,从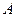 引双曲线的两条渐近线的平行线与直线
引双曲线的两条渐近线的平行线与直线 (
( 为坐标原点)分别交于
为坐标原点)分别交于 和
和 两点.
两点.
(1) 证明:无论 点在什么位置,总有
点在什么位置,总有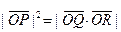 ;
;
(2) 设动点 满足条件:
满足条件:  , 求点
, 求点 的轨迹方程.
的轨迹方程.
(本小题满分12分)
已知点 在抛物线
在抛物线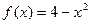 上(如图), 过
上(如图), 过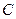 作
作 轴交抛物线于另一点
轴交抛物线于另一点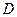 ,设抛物线与
,设抛物线与 轴相交于
轴相交于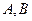 两点,试求
两点,试求 为何值时,梯形
为何值时,梯形 的面积最大,并求出面积的最大值.
的面积最大,并求出面积的最大值.