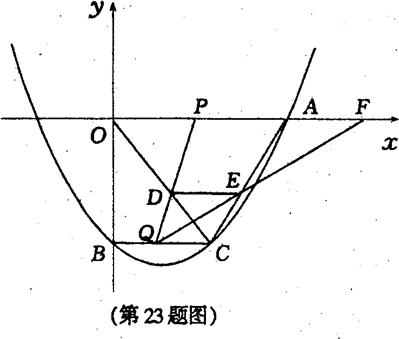
如图，在平面直角坐标系xOy中，抛物线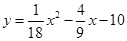与y轴交于点B，过点B-优题课

如图，在平面直角坐标系xOy中，抛物线与y轴交于点B，过点B作x轴的平行线BC，交抛物线于点C，连接AC.现有两动点P，Q分别从0，C两点同时出发，点P以每秒4个单位的速度沿OA向终点A移动，点Q以每秒1个单位速度沿CB向点B移动，点P停止运动时，点Q也同时停止运动，线段OC，PQ相交于点D，过点D作DE∥OA，交CA于点E，射线QE交x辅于点F．设动点P，Q移动的时间为t（单位：秒）．
求A，B，C三点的坐标和抛物线的顶点坐标；
当O<t<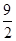时’△PQF的面积是否为定值？若是，求出此定值，若不是，说明理由
当t为何值时，△PQF为等腰三角形？请写出解答过程．

科目数学题型解答题难度中等

知识点：二次函数在给定区间上的最值

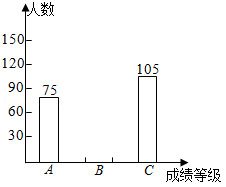
某校开展了“我爱古诗词”知识竞赛活动，将某年级参赛学生的成绩划分为三个等级进行统计分析，绘制得到如图表．

成绩等级	频数	频率
$A$	75	$a$
$B$	$b$	0.4
$C$	105	0.35

请结合图表信息，解答下列问题：

（1）该年级学生共有多少人？

（2）求表中 $a$ ， $b$ 的值，并补全条形统计图；

（3）学校决定从参赛的甲、乙、丙、丁四名同学中任意抽取两名同学做经验介绍，求恰好选中甲、乙两位同学的概率．

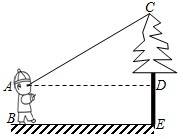
小丽用两锐角分别为 $30 °$ 和 $60 °$ 的三角尺测量一棵树的高度．如图，已知 $∠ CAD = 30 °$ ， $AB = DE = 1.75 m$ ， $BE = 6 m$ ，那么这棵树大约有多高？（结果精确到 $0.1 m$ ， $\sqrt{3} \approx 1.732)$

已知关于 $x$ 的一元二次方程 $x^{2} - 2 x - (k + 1) = 0$ 有两个不相等的实数根，求 $k$ 的取值范围．

（1）计算： ${(π - 2019)}^{0} + | \sqrt{2} - 1 | + 2 \cos 45 °$ ；

（2）计算： $(1 + \frac{1}{x - 1}) \div \frac{x}{x^{2} - 1}$ ．

小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．

（1）温故：如图1，在 $ΔABC$ 中， $AD ⊥ BC$ 于点 $D$ ，正方形 $PQMN$ 的边 $QM$ 在 $BC$ 上，顶点 $P$ ， $N$ 分别在 $AB$ ， $AC$ 上，若 $BC = a$ ， $AD = h$ ，求正方形 $PQMN$ 的边长（用 $a$ ， $h$ 表示）．

（2）操作：如何画出这个正方形 $PQMN$ 呢？

如图2，小波画出了图1的 $ΔABC$ ，然后按数学家波利亚在《怎样解题》中的方法进行操作：先在 $AB$ 上任取一点 $P^{'}$ ，画正方形 $P^{'} Q^{'} M^{'} N^{'}$ ，使点 $Q^{'}$ ， $M^{'}$ 在 $BC$ 边上，点 $N^{'}$ 在 $ΔABC$ 内，然后连结 $B N^{'}$ ，并延长交 $AC$ 于点 $N$ ，画 $NM ⊥ BC$ 于点 $M$ ， $NP ⊥ NM$ 交 $AB$ 于点 $P$ ， $PQ ⊥ BC$ 于点 $Q$ ，得到四边形 $PQMN$ ．

（3）推理：证明图2中的四边形 $PQMN$ 是正方形．

（4）拓展：小波把图2中的线段 $BN$ 称为“波利亚线”，在该线上截取 $NE = NM$ ，连结 $EQ$ ， $EM$ （如图 $3)$ ，当 $∠ QEM = 90 °$ 时，求“波利亚线” $BN$ 的长（用 $a$ ， $h$ 表示）．

请帮助小波解决“温故”、“推理”、“拓展”中的问题．