一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
| 销售方式 |
粗加工后销售 |
精加工后销售 |
| 每吨获利(元) |
1000 |
2000 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多可获得多少利润?此时如何分配加工时间?
已知抛物线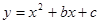 的图象经过点(﹣1,0),点(3,0);
的图象经过点(﹣1,0),点(3,0);
(1)求抛物线函数解析式.
(2)求函数的顶点坐标.
已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.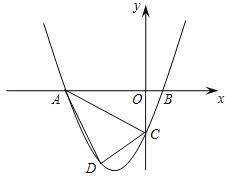
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2.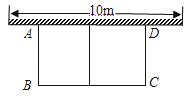
(1)求y与x的函数关系式;
(2)如果要围成面积为63m2的花圃,AB的长是多少?
(3)能围成比63m2更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
某商场将每件进价为80元的某种商品原来按每件100元出售,每天可售出100件,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经过市场调查,发现这种商品售价每降低1元,商场销售量平均每天可增加10件,若商场经营该商品一天要获利润2160元,且让顾客得到实惠,则每件商品应降价多少元?