设边长为2a的正方形的中心A在直线l上,它的一组对边垂直于直线l,半径为r的⊙O的圆心O在直线l上运动,点A,O之间的距离为d。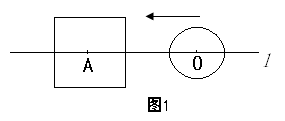
如图1,当r<a时,根据d与a,r之间关系,请你将⊙O与正方形的公共点个数填入下表:
| d,a,r之间的关系 |
公共点的个数 |
| d>a+r |
0 |
| d=a+r |
|
| a-r<d<a+r |
|
| d=a-r |
|
| d<a-r |
|
如图2,当r=a时,根据d与a,r之间关系,请你写出⊙O与正方形的公共点个数,即当r=a时,⊙O与正方形的公共点个数可能有 个。
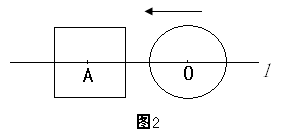
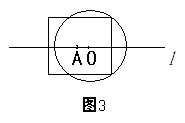
如图3,当⊙O与正方形的公共点个数有5个时,r= (请用a的代数式表示r,不必说明理由)。
计算: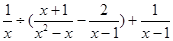
(满分14分)如图,抛物线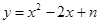 与直线
与直线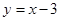 相交于A、B两点(点A在x轴上,点B在y轴上),与x轴的另一个交点为点C.
相交于A、B两点(点A在x轴上,点B在y轴上),与x轴的另一个交点为点C.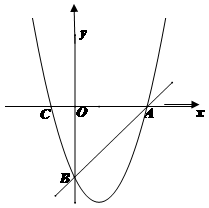
(1)求抛物线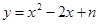 的解析式;
的解析式;
(2)在x轴下方,当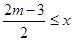 <
<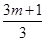 时,抛物线y随x增大而减小,求实数m 的取值范围;
时,抛物线y随x增大而减小,求实数m 的取值范围;
(3)在抛物线上,是否存在点F,使得△BCF是直角三角形?若存在,求出所有满足条件的点F的坐标;若不存在,请说明理由.
(满分14分)几何模型:
如图1, 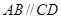 ,O是BD的中点,求证:
,O是BD的中点,求证: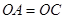 ;
;
模型应用:
(温馨提示:模型应用是指应用模型结论直接解题)
(1)如图2,在梯形ABCD中,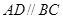 ,点E是腰DC的中点,AE平分
,点E是腰DC的中点,AE平分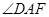 ,求证:AE⊥EF;
,求证:AE⊥EF;
(2)如图3,在⊙O中,AB是⊙O的直径,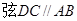 ,点E是OD的中点,点O到AC的距离为1
,点E是OD的中点,点O到AC的距离为1 ,试求阴影部分的面积.
,试求阴影部分的面积. 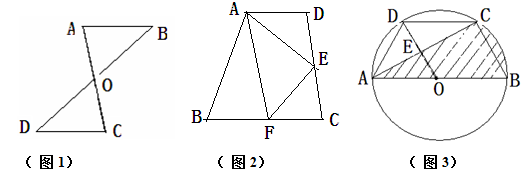
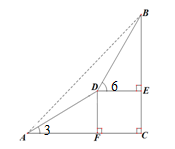
(满分9分)云洞岩被誉为“闽南第一洞天” 风景文化名山,是国家4A级旅游景区。某校数学兴趣小组为测量山高,在山脚A处测得山顶B的仰角为45°,沿着坡角为30°的山坡前进200米到达D处,在D处测得山顶B的仰角为60°,求山的高度BC.(结果保留三个有效数字)(已知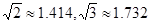 )
)
(满分9分)福建省第15届省运会将于2014年10月在漳州市举行,体训基地欲购买单价为100元的排球和单价为300元的篮球共100个.
(1)如果购买两种球的总费用不超过24000元,并且篮球数不少于排球数的2倍,那么有哪几种购买方案?
(2)从节约开支的角度来看,你认为采用哪种方案最合算?