上海世博会门票价格如下表所示:
| 指定日普通票(张) |
200元 |
| 平日优惠票(张) |
100元 |
某旅行社准备了1300元,全部用来购买指定日普通票和平日优惠票,且每种至少买一张.有多少种购票方案?列举所有可能结果;
如果从上述方案中任意选择一种方案购票,求恰好选到11张门票的概率.
已知一元二次方程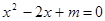 .
.若方程有两个实数根,求m的范围;
若方程的两实根为x1,x2,且
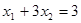 ,求m的值.
,求m的值.
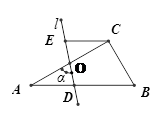
在Rt△ABC中,∠ACB=90°,∠B=60°,BC=4,点O是AC的中点,过点O的直线l从与AC重合的位置开始,绕点O作逆时针旋转,交AB边于点D,过点C作CE∥AB交直线l于E,设直线l的旋转角为α.当α= 时,四边形EDBC是等腰梯形,此时AD= ;
当α= 时,四边形EDBC是直角梯形,此时AD= ;
试判断EDBC能否为菱形,若能,写出此时α的大小,并证明;若不能,请说明理由.
某公司向银行贷款20万元,约定两年到期时一次性还本付息,利息为本金的12%. 该公司用这笔贷款经营,两年到期时除贷款的本、息外还盈利6.4万元,求该公司经营资金的年平均增长率.
如图,在平面直角坐标系xOy中,矩形OEFG的顶点F坐标为(4,2),OG边与y轴重合。将矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,OM
与GF交于点A.判断△OGA和△NPO是否相似,并说明理由;
求过点A的反比例函数解析式;
若(2)中求出的反比例函数的图象与EF交于B点, 请探索:直线AB与OM的位置关系,并说明理由.
在GF所在直线上,是否存在一点Q,使△AOQ为等腰三角形.若存在,请直接写出
所有满足要求的Q点坐标.