已知抛物线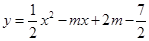
．试说明：无论m为何实数，该抛物线与x轴总有两个不同的交点；
如图，当抛物线的对称轴为直线x=3时，抛物线的顶点为点C，直线y=x﹣1与抛物线交于A、B两点，并与它的对称轴交于点D．
①抛物线上是否存在一点P使得四边形ACPD是正方形？若存在，求出点P的坐标；若不存在，说明理由；
②平移直线CD，交直线AB于点M，交抛物线于点N，通过怎样的平移能使得以C、D、M、N为顶点的四边形是平行四边形？（直接写出平移的方法，不要说明理由）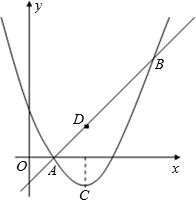
M是大于负50的立方根的最小整数,N是小于50的平方根的最大整数,求M加N的平方根，
已知，如图，点B、F、C、E在同一直线上，AC、DF相交于点G，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AB＝DE，BF＝CE。求证：（1）△ABC≌△DEF；（2）GF＝GC。
（1）计算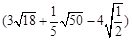
÷
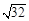；（2）分解因式
．
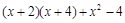在平面直角坐标系
中,已知二次函数
的图象经过点
和点
,直线
经过抛物线的顶点且与
轴垂直,垂足为
.求该二次函数的表达式；
设抛物线上有一动点
从点
处出发沿抛物线向上运动,其纵坐标
随时间
≥
)的变化规律为
.现以线段
为直径作
.
①当点在起始位置点处时,试判断直线与的位置关系,并说明理由；在点运动的过程中,直线与是否始终保持这种位置关系? 请说明你的理由；
②若在点开始运动的同时,直线也向上平行移动,且垂足的纵坐标
随时间
的变化规律为
,则当在什么范围内变化时,直线与相交? 此时,若直线被所截得的弦长为
,试求
的最大值.
知识迁移
当
且
时，因为
≥
,所以
≥,从而
≥
(当
时取等号).
记函数
,由上述结论可知：当时,该函数有最小值为
直接应用
已知函数
与函数
, 则当
____时,
取得最小值为___.
变形应用
已知函数
与函数
,求
的最小值,并指出取得
该最小值时相应的
的值.
实际应用
已知某汽车的一次运输成本包含以下三个部分：一是固定费用,共
元；二是燃油费,每千
米为
元；三是折旧费,它与路程的平方成正比,比例系数为
.设该汽车一次运输的路
程为
千米,求当为多少时,该汽车平均每千米的运输成本最低？最低是多少元？