某港口海水的深度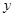 (米)是时间
(米)是时间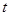 (时)(
(时)(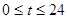 )的函数,记为:
)的函数,记为:
已知某日海水深度的数据如下:
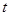 (时) (时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
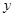 (米) (米) |
10.0 |
13.0 |
9.9 |
7.0 |
10.0 |
13.0 |
10.1 |
7.0 |
10.0 |
经长期观察, 的曲线可近似地看成函数
的曲线可近似地看成函数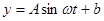 的图象
的图象
(I)试根据以上数据,求出函数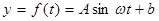 的振幅、最小正周期和表达式;
的振幅、最小正周期和表达式;
(II)一般情况下,船舶航行时,船底离海底的距离为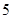 米或
米或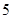 米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可)。某船吃水深度(船底离水面的距离)为
米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可)。某船吃水深度(船底离水面的距离)为 米,如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需时间)
米,如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需时间)
(本小题满分14分)
设直线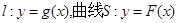 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R,都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R,都有 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
(Ⅰ)已知函数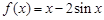 .求证:
.求证: 为曲线
为曲线 的“上夹线”.
的“上夹线”.
(Ⅱ)观察下图:
根据上图,试推测曲线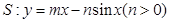 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
(本小题满分13分)
如图,已知椭圆 :
: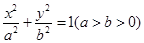 的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点 (4,0)且不与坐标轴垂直的直线
(4,0)且不与坐标轴垂直的直线 交椭圆
交椭圆 于
于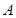 、
、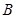 两点,设点
两点,设点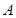 关于
关于 轴的对称点为
轴的对称点为 .
.
(ⅰ)求证:直线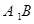 过
过 轴上一定点,并求出此定点坐标;
轴上一定点,并求出此定点坐标;
(ⅱ)求△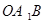 面积的取值范围.
面积的取值范围.
(本小题满分13分)
在数列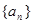 中,其前
中,其前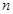 项和
项和 与
与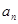 满足关系式:
满足关系式: 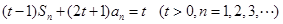 .
.
(Ⅰ)求证:数列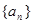 是等比数列;
是等比数列;
(Ⅱ)设数列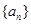 的公比为
的公比为 ,已知数列
,已知数列 ,
,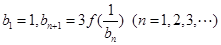 ,求
,求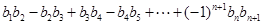 的值.
的值.
(本小题满分13分)
张先生家住H小区,他工作在C科技园区,从家开车到公司上班路上有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为 ,
, .
.
(Ⅰ)若走L1路线,求最多遇到1次红灯的概率;
(Ⅱ)若走L2路线,求遇到红灯次数 的数学期望;
的数学期望;
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助张先生分析上述两条路线中,选择哪条上班路线更好些,并说明理由
(本小题满分13分)
已知 的三个内角
的三个内角 、
、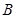 、
、 所对的边分别为
所对的边分别为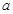 、
、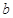 、
、 ,且
,且 ,
, .
.
(Ⅰ)求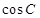 的值;
的值;
(Ⅱ)当 时,求函数
时,求函数 的最大值.
的最大值.