(本小题满分13分)
张先生家住H小区,他工作在C科技园区,从家开车到公司上班路上有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为 ,
, .
.
(Ⅰ)若走L1路线,求最多遇到1次红灯的概率;
(Ⅱ)若走L2路线,求遇到红灯次数 的数学期望;
的数学期望;
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助张先生分析上述两条路线中,选择哪条上班路线更好些,并说明理由
已知数列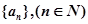 满足
满足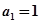 ,且对任意非负整数
,且对任意非负整数 均有:
均有: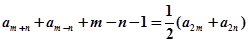 .
.
(1)求 ;
;
(2)求证:数列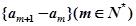 是等差数列,并求
是等差数列,并求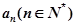 的通项;
的通项;
(3)令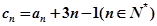 ,求证:
,求证: .
.
已知函数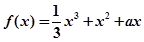 .
.
(1)若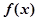 在区间
在区间 单调递增,求
单调递增,求 的最小值;
的最小值;
(2)若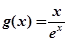 ,对
,对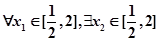 ,使
,使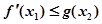 成立,求
成立,求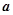 的范围.
的范围.
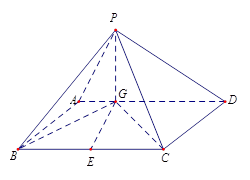
如图四棱锥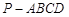 中,底面
中,底面 是平行四边形,
是平行四边形, 平面
平面 ,垂足为
,垂足为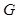 ,
,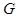 在
在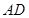 上且
上且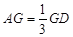 ,
, ,
,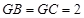 ,
,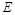 是
是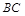 的中点,四面体
的中点,四面体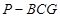 的体积为
的体积为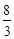 .
.
(1)求二面角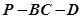 的正切值;
的正切值;
(2)求直线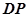 到平面
到平面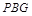 所成角的正弦值;
所成角的正弦值;
(3)在棱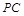 上是否存在一点
上是否存在一点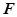 ,使异面直线
,使异面直线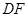 与
与 所成的角为
所成的角为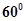 ,若存在,确定点
,若存在,确定点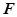 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
成都七中为绿化环境,移栽了银杏树2棵,梧桐树3棵。它们移栽后的成活率分别为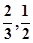 且每棵树是否存活互不影响,求移栽的5棵树中:
且每棵树是否存活互不影响,求移栽的5棵树中:
(1)银杏树都成活且梧桐树成活2棵的概率;
(2)成活的棵树 的分布列与期望.
的分布列与期望.
已知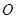 为坐标原点,
为坐标原点,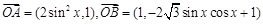 ,
,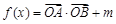 .
.
(Ⅰ)若 的定义域为
的定义域为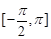 ,求
,求 的单调递增区间;
的单调递增区间;
(Ⅱ)若 的定义域为
的定义域为 ,值域为
,值域为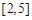 ,求
,求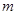 的值.
的值.