在△ 中,
中,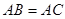 ,
,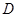 是底边
是底边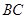 上一点,
上一点,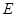 是线段
是线段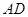 上一点,且
上一点,且
∠ .
.如图1,若∠
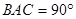 ,猜想
,猜想 与
与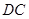 的数量关系为 ;
的数量关系为 ;如图2,若∠
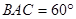 ,猜想
,猜想 与
与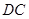 的数量关系,并证明你的结论;
的数量关系,并证明你的结论;若∠
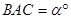 ,请直接写出
,请直接写出 与
与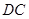 的数量关系.
的数量关系.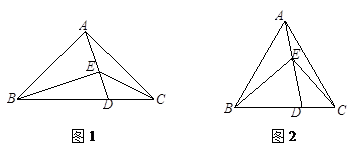
已知:如图,⊙O的直径AB与弦CD相交于E,弧BC=弧BD,CD∥BF,BF交AD的延长线于F。
求证:.BF是⊙O的切线
连结BC,若⊙O的半径为4,cos∠BCD=
 ,求线段AD、CD的长.
,求线段AD、CD的长.
为打造“书香校园”,某学校计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.问符合题意的组建方案有几种?请你帮学校设计出来;
若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明在(1)中哪种方案费用最低?最低费用是多少元?
在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED求证:△BEC≌△DEC;
延长BE交AD于F,当∠BED=120°时,求
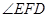 的度数.
的度数.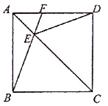
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图像信息,解答下列问题:
这辆汽车的往、返速度是否相同?请说明理由;
求返程中y与x之间的函数表达式;
求这辆汽车从甲地出发4h时与甲地的距离
目前世界上最高的电视塔是广州新电视塔.如图8所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,(sin39°≈0.63,cos39°≈0.78 , tan39°≈0.81)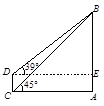
求大楼与电视塔之间的距离AC;
求大楼的高度CD(精确到1米)