已知函数
.
(Ⅰ)若曲线
在点
处的切线平行于
轴,求函数
的单调区间;
(Ⅱ)试确定
的取值范围,使得曲线
上存在唯一的点
,曲线在该点处的切线与曲线只有一个公共点
.
设函数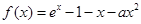 .
.
(1)若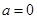 ,求
,求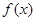 的单调区间;
的单调区间;
(2)若当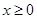 时
时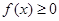 ,求
,求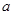 的取值范围
的取值范围
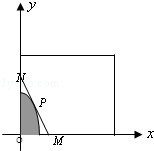
某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线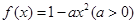 的一部分,栏栅与矩形区域的边界交于点
的一部分,栏栅与矩形区域的边界交于点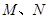 ,交曲线于点
,交曲线于点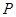 ,设
,设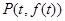 .
.
(1)将△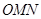 (
(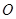 为坐标原点)的面积
为坐标原点)的面积 表示成
表示成 的函数
的函数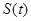 ;
;
(2)若在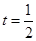 处,
处,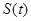 取得最小值,求此时
取得最小值,求此时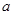 的值及
的值及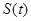 的最小值.
的最小值.
已知数列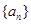 的前
的前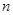 项和为
项和为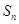 ,常数
,常数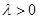 ,且
,且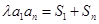 对一切正整数
对一切正整数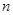 都成立。
都成立。
(Ⅰ)求数列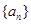 的通项公式;
的通项公式;
(Ⅱ)设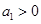 ,
,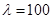 ,当
,当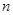 为何值时,数列
为何值时,数列 的前
的前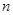 项和最大?
项和最大?
在△ABC中,角A,B,C的对边分别为a,b,c,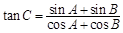 .
.
(1)求角C的大小;
(2)若△ABC的外接圆直径为1,求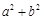 的取值范围.
的取值范围.
已知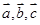 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 .
.
(1)若 ,且
,且 ,求:
,求: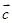 的坐标
的坐标
(2)若 ,且
,且 与
与 垂直,求
垂直,求 与
与 的夹角.
的夹角.