设曲线2x22xyy21在矩阵Aa0b1a<0对应的变换作用-优题课

题文

设曲线 $2 x^{2} + 2 x y + y^{2} = 1$ 在矩阵 $A = (\begin{matrix} a & 0 \\ b & 1 \end{matrix}) (a > 0)$ 对应的变换作用下得到的曲线为 $x^{2} + y^{2} = 1$ .

（Ⅰ）求实数 $a, b$ 的值
（Ⅱ）求 $A^{2}$ 的逆矩阵

科目数学题型解答题难度较易

登录免费查看答案和解析

相关试题

(本小题满分12分)
为了解农民年收入情况，某乡镇对本镇10000户农民按1 0%的比例进行了抽样调查，测得户年收入10000～50000元的情况统计图如下：
(1)估计该镇1万元～2万元的农户数.
(2)估计该镇农户收入在2～4.5万元之间的概率.(将频率看成概率)
(3)如果规定年户收入达不到2.5万元的比例低于25%时，则需要国家政策扶持，请问该乡镇需不需要国家政策扶持？为什么？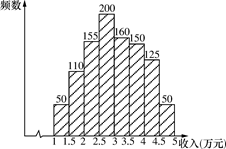

（本小题12分）
某隧道横断面由抛物线和矩形的三边组成，尺寸如图2所示，某卡车载一集装箱，箱宽3m，车与箱共高4m，此车能否通过此隧道？请说明理由．

（本小题12分）
已知顶点在原点，焦点在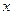轴上的抛物线与直线交于P、Q两点，|PQ|=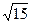，求抛物线的方程

（本小题8分）
若，求证：不可能都是奇数

（本小题10分）
双曲线与椭圆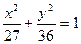有相同焦点，且经过点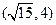，求双曲线的方程

试卷网试题网古诗词网作文网范文网