已知 ,函数
,函数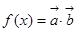 。
。
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求函数 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量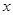 的集合.
的集合.
(本小题满分12分)
已知函数f(x)=2sinωx·cos(ωx+)+(ω>0)的最小正周期为4π.
(1)求正实数ω的值;
(2)在△ABC中,内角A、B、C的对边分别为a、b、c,且满足2bcosA=acosC+ccosA,求f(A)的值.
(本小题满分12分)
若盒中装有同一型号的灯泡共12只,其中有9只合格品,3只次品.
(1)某工人师傅有放回地连续从该盒中取灯泡3次,每次取一只灯泡,求2次取到次品的概率;
(2)某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡前取出的次品灯泡只数X的分布列和数学期望.
选修4-5:不等式选讲
已知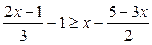 ,求
,求 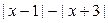 的最大值和最小值.
的最大值和最小值.
选修4—4:坐标系与参数方程
已知直线的极坐标方程为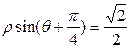 ,圆M的参数方程为
,圆M的参数方程为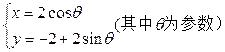 。
。
(1)将直线的极坐标方程化为直角坐标方程;
(2)求圆M上的点到直线的距离的最小值.
选修4-1:几何证明选讲
如图,已知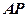 是⊙
是⊙ 的切线,
的切线, 为切点,
为切点,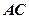 是⊙
是⊙ 的割线,与⊙
的割线,与⊙ 交于
交于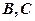 两点,圆心
两点,圆心 在
在 的内部,点
的内部,点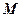 是
是 的中点。
的中点。
(1)证明: 四点共圆;
四点共圆;
(2)求 的大小。
的大小。