小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪两人先下棋,规则:三人手中各持有一枚质地均匀的硬币,他们同时将手中硬币抛落到水平地面为一个回合,落地后,三枚硬币中,恰有两枚正面向上或者反面向上的两人先下棋;若三枚硬币均正面向上或反面向上则不能确定哪两人先下棋。请你完成下面表示游戏一个回合所有可能出现的结果的树状图(你也可自己另外画树状图或列表格);
求一个回合能确定两人先下棋的概率.
如图,在四边形ABCD中,AD=4cm,CD=3cm,AD⊥CD,AB=13cm,BC=12cm,求四边形的面积.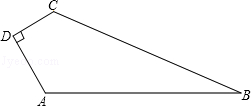
请根据我国古代数学家赵爽的弦图(如图),说明勾股定理.
如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,将△ABC沿AC边所在直线向右平移x个单位,记平移后的对应三角形为△DEF,连接BE.
(1)当x=4时,求四边形ABED的周长;
(2)当x为何值时,△BED是等腰三角形?
如图,在△ABC中,∠BAC=90°,AB=9,AC=12,AD⊥BC,垂足为D.
(1)求BC的长;(2)求BD的长.
如图,在四边形ABCD中,∠DAB=∠DCB=90°,对角线AC与BD相交于点O,M、N分别是边BD、AC的中点.
(1)求证:MN⊥AC;
(2)当AC=8cm,BD=10cm时,求MN的长.