(本小题满分15分)
已知定义在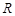 上的函数
上的函数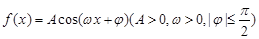 ,最大值与最小值的差为4,相邻两个最低点之间距离为
,最大值与最小值的差为4,相邻两个最低点之间距离为 ,且函数
,且函数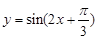 图象所有的对称中心都在
图象所有的对称中心都在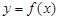 图象的对称轴上.
图象的对称轴上.
(I)求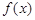 的表达式;
的表达式;
(II)若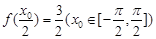 ,求
,求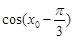 的值;
的值;
(III)设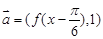 ,
,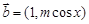 ,
, ,若
,若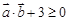 恒成立,求实数
恒成立,求实数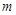 的取值范围.
的取值范围.
(本小题满分10分)选修4—5:不等式选讲
已知函数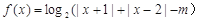 .
.
(1)当 时,求函数
时,求函数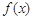 的定义域;
的定义域;
(2)若关于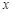 的不等式
的不等式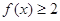 的解集是
的解集是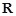 ,求
,求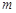 的取值范围.
的取值范围.
(原创)(本小题满分10分)选修4—4:坐标系与参数方程
已知极点与坐标原点重合,极轴与 轴非负半轴重合,
轴非负半轴重合, 是曲线
是曲线 :
: =
= 上任意一点,
上任意一点, =
= ,曲线
,曲线 与直线
与直线 :
: (
( 为参数)相交与
为参数)相交与 ,
, 两点,且|
两点,且| |=
|= .
.
(Ⅰ)求点 的轨迹方程;
的轨迹方程;
(Ⅱ)求实数 的值.
的值.
如图, 为直角三角形,
为直角三角形, ,以AB为直径的圆交AC于点E,点D是BC边的中点,连接OD交圆O于点M,求证:
,以AB为直径的圆交AC于点E,点D是BC边的中点,连接OD交圆O于点M,求证:
(Ⅰ)O、B、D、E四点共圆;
(Ⅱ) .
.
(本小题满分12分)已知函数 ,其中
,其中 为常数,且
为常数,且 .
.
(Ⅰ)若曲线 在点
在点 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值;
(Ⅱ)若函数 在区间
在区间 上的最小值为
上的最小值为 ,求
,求 的值.
的值.
【原创】(本小题满分12分)已知F1、F2是椭圆 的左右焦点,离心率为
的左右焦点,离心率为 ,D是上顶点,C是右顶点,△CDF2的面积为
,D是上顶点,C是右顶点,△CDF2的面积为 .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)若动直线 与椭圆E相交于A、B求△AOB面积的最大值.
与椭圆E相交于A、B求△AOB面积的最大值.