已知点 在由不等式组
在由不等式组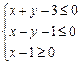 确定的平面区域内,
确定的平面区域内,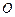 为坐标原点,
为坐标原点, ,试求
,试求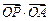 的最大值.
的最大值.
本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多作,则按 所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将选题号填入括号中
所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将选题号填入括号中
(1)选修4一2:矩阵与变换
求矩阵 的特征值及对应的特征向量。
的特征值及对应的特征向量。
(2)选修4一4:坐标系与参数方程
已知直线 的参数方程:
的参数方程: (
( 为参数)和圆
为参数)和圆 的极坐标方程:
的极坐标方程: 。
。
(I)将直线 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(II)判断直线 和圆
和圆 的位置关系
的位置关系
(3)选修4一5:不等式选讲
已知函数 . 若不等式
. 若不等式
 恒成立,求实数
恒成立,求实数 的范围。
的范围。
已知 =
= 是奇函数.
是奇函数.
(1)求m的值
(2)讨论f(x)的单调性
(3)若 ,对于
,对于 ,不等式
,不等式 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。
已知函数 时都取得极值.
时都取得极值.
(I)求a、b的值与函数 的单调区间;
的单调区间;
(II)若对 的取值范围
的取值范围
5.12四川汶川大地震,牵动了全国各地人民的心,为了安置广 大灾民,抗震救灾指挥部决定建造一批简易房(每套长方体状,房高2.5米),前后墙用2.5米高的彩色钢板,两侧用2.5米高的复合钢板,两种钢板的价格都用长度来计算(即:钢板的高均为2.5米,用钢板的长度乘以单价就是这块钢板的价格),每米单价:彩色钢板为450元,复合钢板为200元.房顶用其它材料建造,
大灾民,抗震救灾指挥部决定建造一批简易房(每套长方体状,房高2.5米),前后墙用2.5米高的彩色钢板,两侧用2.5米高的复合钢板,两种钢板的价格都用长度来计算(即:钢板的高均为2.5米,用钢板的长度乘以单价就是这块钢板的价格),每米单价:彩色钢板为450元,复合钢板为200元.房顶用其它材料建造, 每平方米材料费为200元.每套房材料费控制在32000元
每平方米材料费为200元.每套房材料费控制在32000元 以内,试计算:
以内,试计算:
(1)设房前面墙的长为 ,两侧墙的长为
,两侧墙的长为 ,所用材料费为
,所用材料费为 ,试用
,试用 表示
表示 ;
;
(2)求简易房面积S的最大值是多少?并求S最大时,前面墙的长度应设计为多少米?