今年“3.15”期间某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:同一日内,顾客在本商场每消费满200元,就可以在箱子里一次摸出两个球,商场根据两小球所标金额之和返还相应数额的购物券.某顾客刚好消费200元.
(1)该顾客至少可得到 ▲ 元购物券,至多可得到 ▲ 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得的购物券金额不低于30元的概率.
先化简,再求值:(a﹣2b)2﹣3a(a﹣b)+(a+2b)(a﹣2b),其中a=﹣2,b=3.
尺规作图:如图,在Rt△ABC中,∠C=90°.
(1)作斜边AB上的高CD,垂足为D;
(2)作∠A的平分线AE交BC于E(不写作法,保留作图痕迹).
分解因式:16(a+b)2﹣9(a﹣b)2.
某校师生积极为灾区捐款捐物,在得知灾区急需帐篷后,学校采购了两种规格的帐篷;可供3人居住的小帐篷,每顶价格150元,可供10人居住的大帐篷,每顶价格400元.学校花去捐款75000元采购这两种帐篷,正好可供1800人居住.
(1)学校分别采购了多少顶小帐篷和大帐篷?
(2)学校准备租用甲,乙两种运输车共12辆把帐篷运往灾区,已知甲型运输车每辆可同时运15小帐篷8顶大帐篷,乙型运输车可同时运6顶小帐篷16顶大帐篷,学校应该如何安排甲、乙两种型号的运输车可一次性将这批帐篷运往灾区?
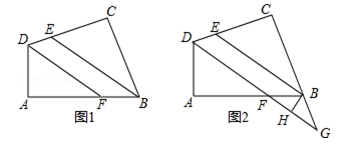
如图1,在四边形ABCD中,∠ABC+∠ADC=180°,BE、DF分别是∠ABC与∠ADC的平分线,∠ADF与∠AFD互余.
(1)试判断直线BE与DF的位置关系,并说明理由;
(2)如图2,延长CB、DF相交于点G,过点B作BH⊥FG,垂足为点H,试判断∠FBH与∠GBH的大小关系,并说明理由.