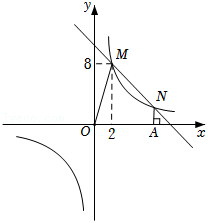
如图,一次函数 与反比例函数 在第一象限交于 、N两点,NA垂直x轴于点A,O为坐标原点,四边形OANM的面积为 .
(1)求反比例函数及一次函数的解析式;
(2)点P是反比例函数第三象限内的图象上一动点,请简要描述使△PMN的面积最小时点P的位置(不需证明),并求出点P的坐标和△PMN面积的最小值.
已知:直角梯形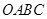 中,
中,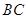 ∥
∥ ,∠
,∠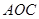 =
=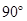 ,以
,以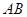 为直径的圆
为直径的圆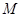 交
交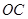 于点
于点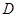 、
、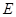 ,连结
,连结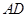 、
、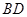 、
、 .
.
(1)在不添加其他字母和线的前提下,直接写出图1中的两对相似三角形:
_____________________,______________________ ;
(2)直角梯形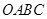 中,以
中,以 为坐标原点,
为坐标原点, 在
在 轴正半轴上建立直角坐标系(如图2),若抛物线
轴正半轴上建立直角坐标系(如图2),若抛物线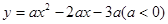 经过点
经过点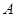 、
、 、
、 ,且
,且 为抛物线的顶点.
为抛物线的顶点.
①写出顶点 的坐标(用含
的坐标(用含 的代数式表示)___________;
的代数式表示)___________;
②求抛物线的解析式;
③在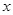 轴下方的抛物线上是否存在这样的点
轴下方的抛物线上是否存在这样的点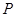 ,过点
,过点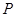 作
作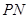 ⊥
⊥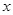 轴于点
轴于点 ,使得以点
,使得以点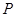 、
、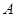 、
、 为顶点的三角形与△
为顶点的三角形与△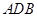 相似?若存在,求出点
相似?若存在,求出点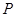 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
某企业为手机产业基地提供手机配件,受人民币走高的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
| 月份x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 价格y1(元/件) |
56 |
58 |
60 |
62 |
64 |
66 |
68 |
70 |
72 |
随着国家调控措施的出台,原材料价格的涨势趋缓,10至12月每件配件的原材料价格y2(元)与月份x(10≤x≤12,且x取整数)之间存在如图所示的变化趋势: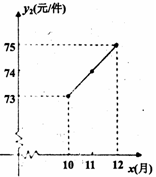
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1与x之间的函数关系式,根据如图所示的变化趋势,直接写出y2与x之间满足的一次函数关系式;
(2)若去年该配件每件的售价为100元,生产每件配件的人力成本为5元,其它成本3元,该配件在1至9月的销售量p1(万件)与月份x满足函数关系式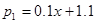 (1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式
(1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式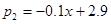 (10≤x≤12,且x取整数)。求去年哪个月销售该配件的利润最大,并求出这个最大利润;
(10≤x≤12,且x取整数)。求去年哪个月销售该配件的利润最大,并求出这个最大利润;
(3)今年1月,每件配件的原材料价格比去年12月上涨6元,人力成本比去年增加20%,其它成本没有变化,该企业将每件配件的售价在去年的基础上提高a%,与此同时1月份销售量在去年12月的基础上减少8a%,这样,在保证1月份上万件配件销量的前提下,完成了利润17万元的任务,请你计算出a的值。
某地为了了解当地推进“阳光体育”运动情况,就“中小学每天在校体育活动时间”的问题随机调查了300名中小学生.根据调查结果绘制成的统计图的一部分如图(其中分组情况见表):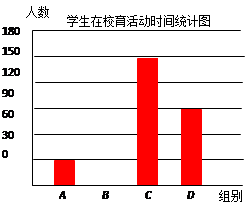
| 组别 |
范围(小时) |
| A |
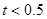 |
| B |
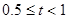 |
| C |
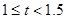 |
| D |
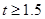 |
请根据上述信息解答下列问题:
(1)B组的人数是人;
(2)本次调查数据(指体育活动时间)的中位数落在组内;
(3)若某地约有64000名中小学生,请你估计其中达到国家规定体育活动时间(不低于1小时)的人数约有多少?
已知,在平面直角坐标系中,直线 :
: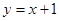 与直线
与直线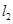 :
: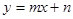 相交于点
相交于点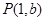 .
.
(1)求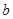 的值;
的值;
(2)不解关于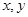 的方程组
的方程组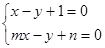 ,请你直接写出它的解。
,请你直接写出它的解。
暴雨过后,某地遭遇山体滑坡,武警总队派出一队武警战士前往抢险. 半小时后,第二队前去支援,平均速度是第一队的1.5倍,结果两队同时到达.已知抢险队的出发地与灾区的距离为90千米,两队所行路线相同,问两队的平均速度分别是多少?