如图,抛物线 交x轴于 ,B两点,交y轴于点 ,顶点D的横坐标为 .
(1)求抛物线的解析式;
(2)在y轴的负半轴上是否存在点P使 ,若存在,求出点P的坐标,若不存在,请说明理由;
(3)过点C作直线l与y轴垂直,与抛物线的另一个交点为E,连接AD,AE,DE,在直线l下方的抛物线上是否存在一点M,过点M作 ,垂足为F,使以M,F,E三点为顶点的三角形与△ADE相似?若存在,请求出M点的坐标,若不存在,请说明理由.
某校开展校园艺术节系列活动,派小明到文体超市购买若干个文具袋作为奖品.这种文具袋标价每个10元,请认真阅读结账时老板与小明的对话:

(1)结合两人的对话内容,求小明原计划购买文具袋多少个?
(2)学校决定,再次购买钢笔和签字笔共50支作为补充奖品,两次购买奖品总支出不超过400元.其中钢笔标价每支8元,签字笔标价每支6元,经过沟通,这次老板给予8折优惠,那么小明最多可购买钢笔多少支?
赤峰市某中学为庆祝"世界读书日",响应"书香校园"的号召,开展了"阅读伴我成长"的读书活动.为了解学生在此次活动中的读书情况,从全校学生中随机抽取一部分学生进行调查,将收集到的数据整理并绘制成如图所示不完整的折线统计图和扇形统计图.
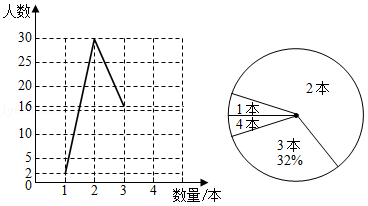
(1)随机抽取学生共 名,2本所在扇形的圆心角度数是 度,并补全折线统计图;
(2)根据调查情况,学校决定在读书数量为1本和4本的学生中任选两名学生进行交流,请用树状图或列表法求这两名学生读书数量均为4本的概率.
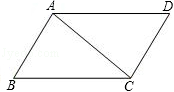
已知: AC是▱ ABCD的对角线.
(1)用直尺和圆规作出线段 AC的垂直平分线,与 AD相交于点 E,连接 CE.(保留作图痕迹,不写作法);
(2)在(1)的条件下,若 AB=3, BC=5,求△ DCE的周长.
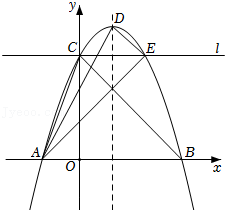
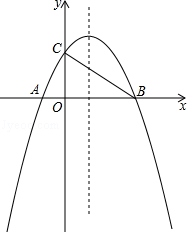
如图,在平面直角坐标系中,已知抛物线 y= ax 2+ bx+2( a≠0)与 x轴交于 A(﹣1,0), B(3,0)两点,与 y轴交于点 C,连接 BC.
(1)求该抛物线的解析式,并写出它的对称轴;
(2)点 D为抛物线对称轴上一点,连接 CD、 BD,若∠ DCB=∠ CBD,求点 D的坐标;
(3)已知 F(1,1),若 E( x, y)是抛物线上一个动点(其中1< x<2),连接 CE、 CF、 EF,求△ CEF面积的最大值及此时点 E的坐标.
(4)若点 N为抛物线对称轴上一点,抛物线上是否存在点 M,使得以 B, C, M, N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点 M的坐标;若不存在,请说明理由.
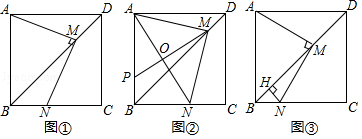
如图,在正方形 ABCD中, AB=6, M是对角线 BD上的一个动点(0< DM< BD),连接 AM,过点 M作 MN⊥ AM交 BC于点 N.
(1)如图①,求证: MA= MN;
(2)如图②,连接 AN, O为 AN的中点, MO的延长线交边 AB于点 P,当 时,求 AN和 PM的长;
(3)如图③,过点 N作 NH⊥ BD于 H,当 AM=2 时,求△ HMN的面积.