赤峰市某中学为庆祝"世界读书日",响应"书香校园"的号召,开展了"阅读伴我成长"的读书活动.为了解学生在此次活动中的读书情况,从全校学生中随机抽取一部分学生进行调查,将收集到的数据整理并绘制成如图所示不完整的折线统计图和扇形统计图.
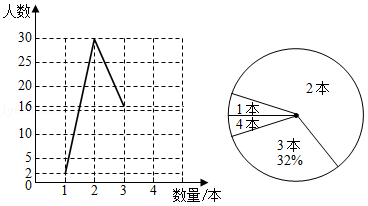
(1)随机抽取学生共 名,2本所在扇形的圆心角度数是 度,并补全折线统计图;
(2)根据调查情况,学校决定在读书数量为1本和4本的学生中任选两名学生进行交流,请用树状图或列表法求这两名学生读书数量均为4本的概率.
下面是解分式方程的过程,阅读完后请填空.
解方程: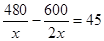 .
.
解:方程两边都乘以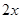 ,得
,得
960 - 600=90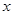 ,
,
解这个方程,得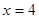 .
.
经检验,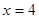 是原方程的根.
是原方程的根.
第一步计算中的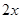 是: ;这个步骤用到的依据是 ;
是: ;这个步骤用到的依据是 ;
解方式方程与解一元一次方程之间的联系是: .
如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N.其顶点为D.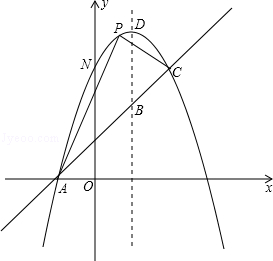
(1)抛物线及直线AC的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
如图:三角形ABC内接于圆O,∠BAC与∠ABC的角平分线AE,BE相交于点E,延长AE交外接圆O于点D,连接BD,DC,且∠BCA=60°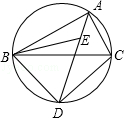
(1)求∠BED的大小;
(2)证明:△BED为等边三角形;
(3)若∠ADC=30°,圆O的半径为r,求等边三角形BED的边长.
某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.请比较哪种方案的最大利润更高,并说明理由.
如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字,现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).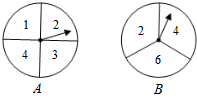
(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;
(2)李刚为甲、乙两人设计了一个游戏:记s=x+y.当s<6时,甲获胜,否则乙获胜.你认为这个游戏公平吗?对谁有利?
(3)请你利用两个转盘,设计一个公平的游戏规则.