已知椭圆C的中心在坐标原点,焦点在 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线 的焦点,离心率为
的焦点,离心率为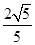 .
.
(1)求椭圆C的标准方程;
(2)过椭圆C的右焦点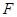 作直线
作直线 交椭圆C于
交椭圆C于 、
、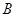 两点,交
两点,交 轴于
轴于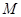 点,若
点,若 ,
,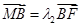 ,求证:
,求证: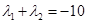 .
.
解不等式组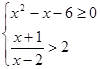 .
.
(本小题满分10分)已知函数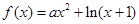
(1)若函数 在区间
在区间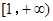 上为减函数,求实数
上为减函数,求实数 的取值范围
的取值范围
(2)当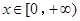 时,不等式
时,不等式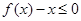 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
(本小题满分10分)已知椭圆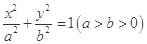 的两个焦点为
的两个焦点为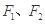 ,离心率为
,离心率为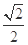 ,直线l与椭圆相交于A、B两点,且满足
,直线l与椭圆相交于A、B两点,且满足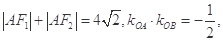
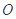 为坐标原点.
为坐标原点.
(1)求椭圆的方程;
(2)证明: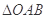 的面积为定值.
的面积为定值.
(本小题满分10分)在平面直角坐标系 中,点
中,点 ,直线
,直线 ,设圆
,设圆 的半径为
的半径为 ,圆心在
,圆心在 上.
上.
(1)若圆心 也在直线
也在直线 上,过点
上,过点 作圆
作圆 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆 上存在点
上存在点 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围.
的取值范围.
(文)如图,已知四边形ABCD为矩形, 平面ABE,AE=EB=BC=2,F为CE上的点,且
平面ABE,AE=EB=BC=2,F为CE上的点,且 平面ACE.
平面ACE.
(1)求证:AE//平面BDF;
(2)求三棱锥D-ACE的体积.