设ζ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两-优题课

题文

设 $ζ$ 为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时， $ζ = 0$ ；当两条棱平行时， $ζ$ 的值为两条棱之间的距离；当两条棱异面时， $ζ = 1$ ．
（1）求概率 $P (ζ = 0)$ ；
（2）求 $ζ$ 的分布列，并求其数学期望

科目数学题型解答题难度容易

相关试题

已知函数．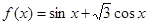
求函数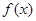的最小正周期；
求函数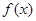的最值及取到最小值的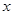的集合．

有甲、乙两个班，进行数学考试，按学生考试及格与不及格统计成绩后，得到如下的列联表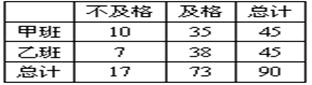

根据表中数据，你有多大把握认为成绩及格与班级有关？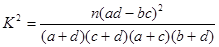
附表：

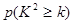	0.050	0.010	0.001
k	3.841	6.635	10.828

选修4—5:不等式选讲
已知函数。
（ I）当a=－3时，求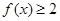的解集；
（Ⅱ）当f（x）定义域为R时，求实数a的取值范围

已知直线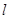的参数方程为为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为．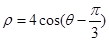
（I）判断直线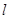与圆C的位置关系；
（Ⅱ）若点P（x，y）在圆C上，求x +y的取值范围．

如图，AB是⊙O的直径，C、E为⊙O上的点，CA平分∠BAE，CF⊥AB， F是垂足，CD⊥AE，交AE延长线于D．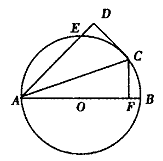

（I）求证：DC是⊙O的切线；
（Ⅱ）求证：AF．FB=DE．DA．