如图,在□ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C.
试说明:△ABF∽△EAD;
若AB=4,BE=3,AD=3,求BF的长.
已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点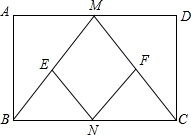
(1)求证:△ABM≌△DCM
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB=_时,四边形MENF是正方形(只写结论,不需证明)
如图,马路的两边CF、DE互相平行,线段CD为人行横道,马路两侧的A、B两点分别表示车站和超市。CD与AB所在直线互相平行,且都与马路两边垂直,马路宽20米,A,B相距62米,
∠A=67°,∠B=37°
(1)求CD与AB之间的距离;
(2)某人从车站A出发,沿折线A→D→C→B去超市B,求他沿折线A→D→C→B到达超市比直接横穿马路多走多少米
(参考数据: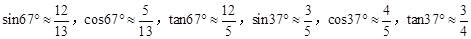 )
)
某校学生捐款支援地震灾区,第一次捐款总额为6600元,第二次捐款总额为7260元,第二次捐款人数比第一次多30人,而且两次人均捐款额恰好相等,求第一次的捐款人数
小明和小刚做纸牌游戏,如图,两组相同的纸牌,每组两张,牌面数字分别是2和3,将两组牌背面朝上,洗匀后从每组牌中各抽取一张,称为一次游戏。当两张牌的牌面数字之和为奇数,小明得2分,否则小刚得1分,这个游戏对双方公平吗?请说明理由
请根据所给信息,帮助小颖同学完成她的调查报告
2013年4月光明中学八年级学生每天干家务活平均时间的调查报告
| 调查目的 |
了解八年级学生每天干家务活的平均时间 |
||||||||||||||||||||||||||||||
| 调查内容 |
光明中学八年级学生每天干家务活的平均时间 |
||||||||||||||||||||||||||||||
| 调查方式 |
抽样调查 |
||||||||||||||||||||||||||||||
| 调查步骤 |
1、数据的收集: (1)在光明中学八年级每班随机调查5名学生; (2)统计这些学生2013年4月每天干家务活的平均时间(单位:min),结果如下(其中A表示10min;B表示20min;C表示30min);
2、数据的处理: |
||||||||||||||||||||||||||||||
| 调查结论 |
光明中学八年级共有240名学生,其中大约有 名学生每天干家务活的平均时间是20min …… |