(本小题满分l2分)已知数列{an}中,a1=1,a2=3且2an+1=an+2+an(n∈N*).数列{bn}的前n项和为Sn,其中b1=-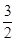 ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*).
(1)求数列{an}和{bn}的通项公式;
(2)若Tn=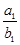 +
+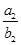 +…+
+…+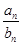 ,求Tn的表达式
,求Tn的表达式
已知点(1,2)是函数 的图象上一点,数列
的图象上一点,数列 的前
的前 项和
项和 .
.
(Ⅰ)求数列 的通项公式
的通项公式
(Ⅱ)若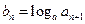 ,求数列
,求数列 的前
的前 项和
项和 .
.
如图,海中小岛A周围40海里内有暗礁,一船正在向南航行,在B处测得小岛A在船的南偏东30°,航行30海里后,在C处测得小岛在船的南偏东45°,如果此船不改变航向,继续向南航行,问有无触礁的危险?
在△ABC中,角A、B、C的对边分别为a、b、c,且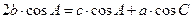
(Ⅰ)求角A的大小;
(Ⅱ)若 ,求△ABC的面积.
,求△ABC的面积.
已知集合 ,
,
(Ⅰ)当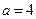 时,求
时,求
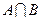 (Ⅱ)若
(Ⅱ)若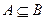 ,求实数
,求实数 的取值范围.
的取值范围.
已知指数函数 满足:g(3)=8,定义域为
满足:g(3)=8,定义域为 的函数
的函数 是奇函数.
是奇函数.
(1)确定 的解析式;
的解析式;
(2)求m,n的值;
(3)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围