本题共有2个小题,第1小题满分6分,第2小题满分8分。已知数列 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为 ,
, 为其前
为其前 项和,且满足
项和,且满足 ,
, .数列
.数列 满足
满足 ,
, 为数列
为数列 的前n项和.
的前n项和.
(1)求 、
、 和
和 ;
;
(2)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
(本小题满分12分)
已知函数 在点
在点 处的切线方程是
处的切线方程是 ,其中
,其中 是自然对数的底数.
是自然对数的底数.
(1)求实数a、b的值;
(2)求函数 在区间
在区间 上的值域.
上的值域.
(本小题满分12分)已知向量 ,
, ,
, ,且
,且 .
.
(1)求 ;
;
(2)设向量 与
与 的夹角为
的夹角为 ,求
,求 的值.
的值.
(本小题满分12分)
在各项均为正数的等比数列 中,
中,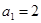 ,且
,且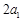 ,
,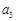 ,
,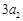 成等差数列.
成等差数列.
(1)求等比数列 的通项公式;
的通项公式;
(2)若数列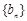 满足
满足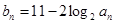 ,求数列
,求数列 的前n项和
的前n项和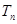 的最大值.
的最大值.
已知函数f(x)=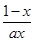 +lnx(a>0)
+lnx(a>0)
(1)若函数f(x)在[1,+∞)上为增函数,求实数a的取值范围;
(2)当a=1时,求f(x)在[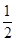 ,2]上的最大值和最小值.
,2]上的最大值和最小值.
已知函数f(x)=x(x+a)-lnx,其中a为常数.
(1)求f(x)的单调区间;
(2)过坐标原点可以坐几条直线与曲线y=f(x)相切?说明理由.