本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分。
定义:对函数 ,对给定的正整数
,对给定的正整数 ,若在其定义域内存在实数
,若在其定义域内存在实数 ,使得
,使得 ,则称函数
,则称函数 为“
为“ 性质函数”。
性质函数”。
(1)判断函数 是否为“
是否为“ 性质函数”?说明理由;
性质函数”?说明理由;
(2)若函数 为“2性质函数”,求实数
为“2性质函数”,求实数 的取值范围;
的取值范围;
(3)已知函数 与
与 的图像有公共点,求证:
的图像有公共点,求证: 为“1性质函数”。
为“1性质函数”。
一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
如图所示,设铁路AB=50,B、C之间距离为10,现将货物从A运往C,已知单位距离铁路费用为2,公路费用为4,问在AB上何处修筑公路至C,可使运费由A到C最省?
某种产品每件成本为6元,每件售价为x元(x>6),年销量为u万件,若已知 与
与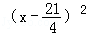 成正比,且售价为10元时,年销量为28万件.
成正比,且售价为10元时,年销量为28万件.
(1)求年销售利润y关于x的函数关系式.
(2)求售价为多少时,年利润最大,并求出最大年利润.
用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少?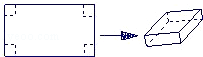
对于5年可成材的树木,从栽种到5年成材的木材年生长率为18%,以后木材的年生长率为10%.树木成材后,既可以出售树木,重栽新树苗;也可以让其继续生长.问:哪一种方案可获得较大的木材量?(注:只需考虑10年的情形)(参考数据:lg2=0.3010,lg1.1=0.0414)