(本小题满分16分)已知函数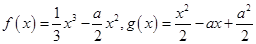 .
.
(1)当 时,求曲线
时,求曲线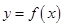 在点
在点 处的切线方程;
处的切线方程;
(2)当函数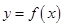 在区间
在区间 上的最小值为
上的最小值为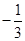 时,求实数
时,求实数 的值;
的值;
(3)当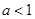 时,若函数
时,若函数 与
与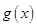 的图像有三个不同的交点,求实数
的图像有三个不同的交点,求实数 的取值范围.
的取值范围.
设 ,
,
(1)在下列直角坐标系中画出 的图象;
的图象;
(2)若 ,求
,求 值。
值。
已知
(1)求 的值,
的值,
(2)求 的值。
的值。
正项数列{ }的前n项和为Sn,q为非零常数.已知对任意正整数n, m,当
}的前n项和为Sn,q为非零常数.已知对任意正整数n, m,当 时
时 总成立.
总成立.
(1)求证:数列{ }是等比数列;
}是等比数列;
(2)若互不相等的正整数n, m, k成等差数列,比较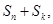
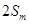 的大小;
的大小;
(3)(限理科生做,文科生不做)若正整数n, m, k成等差数列,求证: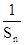 +
+ ≥
≥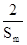 .
.
设椭圆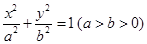 的左、右顶点分别为
的左、右顶点分别为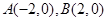 ,离心率
,离心率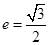 .过该椭圆上任一点
.过该椭圆上任一点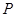 作
作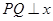 轴,垂足为
轴,垂足为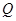 ,点
,点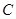 在
在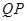 的延长线上,且
的延长线上,且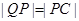 .
.
(1)求椭圆的方程;
(2)求动点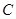 的轨迹
的轨迹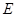 的方程;
的方程;
(3)设直线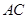 (
(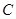 点不同于
点不同于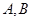 )与直线
)与直线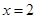 交于点
交于点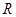 ,
,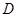 为线段
为线段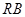 的中点,试判断直线
的中点,试判断直线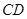 与曲线
与曲线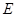 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
如下图,互相垂直的两条公路 、
、 旁有一矩形花园
旁有一矩形花园 ,现欲将其扩建成一个更
,现欲将其扩建成一个更
大的三角形花园 ,要求点
,要求点 在射线
在射线 上,点
上,点 在射线
在射线 上,且直线
上,且直线 过点
过点 ,其中
,其中 米,
米, 米.记三角形花园
米.记三角形花园 的面积为
的面积为 .
.
(1)问: 取何值时,
取何值时, 取得最小值,并求出最小值;
取得最小值,并求出最小值;
(2)若 不超过1764平方米,求
不超过1764平方米,求 长的取值范围.
长的取值范围.