正项数列{ }的前n项和为Sn,q为非零常数.已知对任意正整数n, m,当
}的前n项和为Sn,q为非零常数.已知对任意正整数n, m,当 时
时 总成立.
总成立.
(1)求证:数列{ }是等比数列;
}是等比数列;
(2)若互不相等的正整数n, m, k成等差数列,比较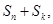
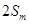 的大小;
的大小;
(3)(限理科生做,文科生不做)若正整数n, m, k成等差数列,求证: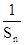 +
+ ≥
≥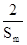 .
.
甲乙丙三人参加一家公司的招聘面试,面试合格者可正式签约。甲表示只要面试合格就签约,乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约。设每人面试合格的概率都是
,且面试是否合格互不影响。求:
(I)至少一人面试合格的概率;
(II)没有人签约的概率。
(本小题满分10分)选修4-4;坐标系与参数方程
在直角坐标第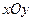 中,直线
中,直线 的参数方程为:
的参数方程为: (
(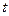 为参数),若以
为参数),若以 为极点,
为极点, 轴正半轴为极轴建立极坐标系,则曲线
轴正半轴为极轴建立极坐标系,则曲线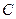 的极坐标方程为
的极坐标方程为 ,求直线
,求直线 被曲线
被曲线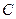 所截的弦长。
所截的弦长。
(本小题满分10分)选修4-1:几何证明选讲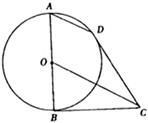
如图所示,AB为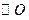 的直径,BC、CD为
的直径,BC、CD为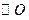 的切线,B、D为切点。
的切线,B、D为切点。
(1)求证:AD//OC;
(2)若圆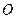 的半径为1,求AD·OC的值。
的半径为1,求AD·OC的值。
(本小题满分12分)
已知点 ,B、C在
,B、C在 轴上,且
轴上,且 ,
,
(1)求 外心的轨迹
外心的轨迹 的方程;
的方程;
(2)若P、Q为轨迹S上两点,求实数 范围,使
范围,使 ,且
,且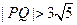 。
。
(本小题满分12分)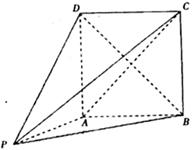
如图,在几何体 中,四边形
中,四边形 为矩形,
为矩形,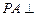 平面
平面 ,
, 。
。
(1)当 时,求证:平面
时,求证:平面 平面
平面 ;
;
(2)若 与
与 所成角为45°,求几何体
所成角为45°,求几何体 的体积。
的体积。