商场某种商品平均每天可销售30件,每件盈利50元. 为了尽快减少库存,商场决定采取适当的降价措施. 经调查发现,每件商品每降价1元,商场平均每天可多售出 2件.设每件商品降价x元. 据此规律,请回答:商场日销售量增加 件,每件商品盈利 元(用含x的代数式表示);
在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
(本小题满分10分)某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,请你估计该校八年级汉字书写优秀的人数?
(4)第一组中的A、B、C、D 四名同学为提高汉字书写能力,分成两组,每组两人进行对抗练习,请用列表法或画树状图的方法,求A与B名同学能分在同一组的概率.
(本小题满分10分)已知代数式:A=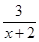 ,B=
,B=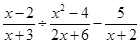 .
.
(1)试证明:若A、B均有意义,则它们的值互为相反数;
(2)若代数式A、B中的x是满足不等式3(x-3)<6-2x的正整数解,求A-B的值.
如图,已知抛物线 与x轴交于A(-2,0)、B两点,与y轴交于C点,其对称轴为直线
与x轴交于A(-2,0)、B两点,与y轴交于C点,其对称轴为直线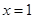 .
.
(1)求抛物线的解析式;
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,若存在,求出E、F的坐标;若不存在,请说明理由.
如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的矩形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D,旋转角为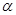 .
.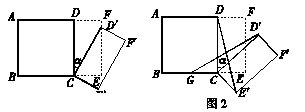
(1)当点D′恰好落在EF边上时,则旋转角α的值为________度;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,是否存在旋转角α,使△DCD′与△CBD′全等?若能,直接写出旋转角α的值;若不能,说明理由.
如图,点C在⊙O的直径AB的延长线上,点D在⊙O上,AD=CD,∠ADC=120°.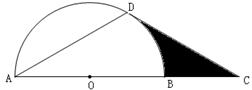
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.