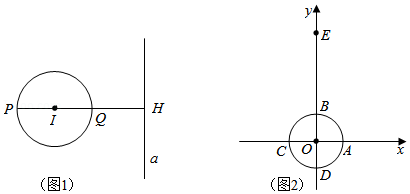解方程组：．-优题课

某停车场的收费标准如下：中型汽车的停车费为15元 $/$ 辆，小型汽车的停车费为8元 $/$ 辆．现在停车场内停有30辆中、小型汽车，这些车共缴纳停车费324元，求中、小型汽车各有多少辆？

解不等式 $2 x - 1 > \frac{3 x - 1}{2}$ ．

解：去分母，得 $2 (2 x - 1) > 3 x - 1$ ．

$\dots$

（1）请完成上述解不等式的余下步骤：

（2）解题回顾：本题“去分母”这一步的变形依据是　　（填“ $A$ ”或“ $B$ ” $)$ ．

$A$ ．不等式两边都乘（或除以）同一个正数，不等号的方向不变；

$B$ ．不等式两边都乘（或除以）同一个负数，不等号的方向改变．

计算：

（1） $| - 3 | + {(π - 1)}^{0} - \sqrt{4}$ ；

（2） $\frac{x + 1}{2 x} \div (1 + \frac{1}{x})$ ．

如图，二次函数 $y = x^{2} + bx + 3$ 的图象与 $y$ 轴交于点 $A$ ，过点 $A$ 作 $x$ 轴的平行线交抛物线于另一点 $B$ ，抛物线过点 $C (1, 0)$ ，且顶点为 $D$ ，连接 $AC$ 、 $BC$ 、 $BD$ 、 $CD$ ．

（1）填空： $b =$ 　　；

（2）点 $P$ 是抛物线上一点，点 $P$ 的横坐标大于1，直线 $PC$ 交直线 $BD$ 于点 $Q$ ．若 $∠ CQD = ∠ ACB$ ，求点 $P$ 的坐标；

（3）点 $E$ 在直线 $AC$ 上，点 $E$ 关于直线 $BD$ 对称的点为 $F$ ，点 $F$ 关于直线 $BC$ 对称的点为 $G$ ，连接 $AG$ ．当点 $F$ 在 $x$ 轴上时，直接写出 $AG$ 的长．

如图1， $⊙ I$ 与直线 $a$ 相离，过圆心 $I$ 作直线 $a$ 的垂线，垂足为 $H$ ，且交 $⊙ I$ 于 $P$ 、 $Q$ 两点 $(Q$ 在 $P$ 、 $H$ 之间）．我们把点 $P$ 称为 $⊙ I$ 关于直线 $a$ 的“远点“，把 $PQ \cdot PH$ 的值称为 $⊙ I$ 关于直线 $a$ 的“特征数”．

（1）如图2，在平面直角坐标系 $xOy$ 中，点 $E$ 的坐标为 $(0, 4)$ ．半径为1的 $⊙ O$ 与两坐标轴交于点 $A$ 、 $B$ 、 $C$ 、 $D$ ．

①过点 $E$ 画垂直于 $y$ 轴的直线 $m$ ，则 $⊙ O$ 关于直线 $m$ 的“远点”是点　　（填“ $A$ ”．“ $B$ ”、“ $C$ ”或“ $D$ ” $)$ ， $⊙ O$ 关于直线 $m$ 的“特征数”为　　；

②若直线 $n$ 的函数表达式为 $y = \sqrt{3} x + 4$ ．求 $⊙ O$ 关于直线 $n$ 的“特征数”；

（2）在平面直角坐标系 $xOy$ 中，直线 $l$ 经过点 $M (1, 4)$ ，点 $F$ 是坐标平面内一点，以 $F$ 为圆心， $\sqrt{2}$ 为半径作 $⊙ F$ ．若 $⊙ F$ 与直线 $l$ 相离，点 $N (- 1, 0)$ 是 $⊙ F$ 关于直线 $l$ 的“远点”．且 $⊙ F$ 关于直线 $l$ 的“特征数”是 $4 \sqrt{5}$ ，求直线 $l$ 的函数表达式．