已知函数 (
(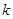 为常数,
为常数,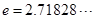 是自然对数的底数),曲线
是自然对数的底数),曲线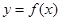 在点
在点 处的切线与
处的切线与 轴平行.
轴平行.
(Ⅰ)求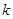 的值;
的值;
(Ⅱ)求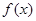 的单调区间;
的单调区间;
(Ⅲ)设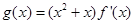 ,其中
,其中 为
为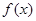 的导函数.证明:对任意
的导函数.证明:对任意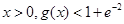 .
.
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在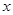 轴上,离心率为
轴上,离心率为 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线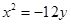 的焦点.
的焦点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点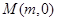 的直线
的直线 与椭圆
与椭圆 相切
相切 ,直线
,直线 与
与 轴交于点
轴交于点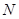 ,当
,当 为何值时
为何值时 的面积有最小值?并求出最小值.
的面积有最小值?并求出最小值.
已知函数 ·
· (其中
(其中 >o),且函数
>o),且函数 的最小正周期为
的最小正周期为
(I)求f(x)的最大值及相应x的取值
(Ⅱ)将函数y= f(x)的图象向左平移 单位长度,再将所得图象各点的横坐标缩小为原来的
单位长度,再将所得图象各点的横坐标缩小为原来的 倍(纵坐标不变)得到函数y=g(x)的图象.求函数g(x)的单调区间.
倍(纵坐标不变)得到函数y=g(x)的图象.求函数g(x)的单调区间.
如图所示,在四棱锥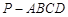 中,底面
中,底面 为矩形,
为矩形,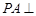 平面
平面 ,点
,点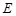 在线段
在线段 上,
上,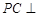 平面
平面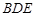 .
.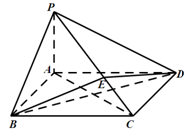
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)若 ,
,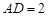 ,求二面角
,求二面角 的正切值.
的正切值.
某高校在2013年考试成绩中100名学生的笔试成绩的频率分布直方图如图所示,
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
① 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙不同时进入第二轮面试的概率;
② 若第三组被抽中的学生实力相当,在第二轮面试中获得优秀的概率均为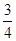 ,设第三组中被抽中的学生有
,设第三组中被抽中的学生有 名获得优秀,求
名获得优秀,求 的分布列和数学期望。
的分布列和数学期望。