(本小题满分14分) 设函数 .
.
(Ⅰ)当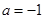 时,求函数
时,求函数 的单调区间和极大值点;
的单调区间和极大值点;
(Ⅱ)已知 ,若函数
,若函数 的图象总在直线
的图象总在直线 的下方,求
的下方,求 的取值范围;
的取值范围;
(Ⅲ)记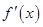 为函数
为函数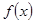 的导函数.若
的导函数.若 ,试问:在区间
,试问:在区间 上是否存在
上是否存在 (
(
 )个正数
)个正数 …
… ,使得
,使得 成立?请证明你的结论.
成立?请证明你的结论.
求经过点A(5,2),B(3,2),圆心在直线2x﹣y﹣3=0上圆的标准方程.
如图,已知三棱柱ABC﹣A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2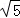 ,设这条最短路线与交于点D.
,设这条最短路线与交于点D.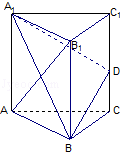
(1)求三棱柱ABC﹣A1B1C1的棱长;
(2)求四棱锥A1﹣BCC1B1的体积;
(3)在平面A1BD内是否存在过点D的直线与平面ABC平行?并说明理由.
(Ⅰ)求过点(1,﹣1),且与直线x+4y﹣7=0垂直的直线方程.
(Ⅱ)求过点(1,﹣1),且与直线x+4y﹣7=0平行的直线方程.
假设你家订了一份报纸,送报人可能在早上6点—8点之间把报纸送到你家,你每天离家去工作的时间在早上7点—9点之间
(1)你离家前不能看到报纸(称事件A)的概率是多少?(8分,须有过程)
(2)请你设计一种随机模拟的方法近似计算事件A的概率(包括手工的方法或用计算器、计算机的方法)
已知在平面直角坐标系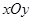 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为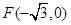 ,右顶点为
,右顶点为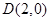 ,设点
,设点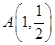 .
.
(1)求该椭圆的标准方程;
(2)若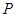 是椭圆上的动点,求线段
是椭圆上的动点,求线段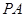 中点
中点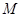 的轨迹方程;
的轨迹方程;