如图,在四棱锥 中,四边形
中,四边形 为平行四边形,
为平行四边形, ,
, ,
, 为
为 上一点,且
上一点,且 平面
平面 .
.
⑴求证: ;
;
⑵如果点 为线段
为线段 的中点,求证:
的中点,求证: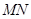 ∥平面
∥平面 .
.
已知数列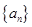 的各项均大于1,前n项和
的各项均大于1,前n项和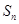 满足
满足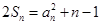 。
。
(Ⅰ)求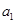 及数列
及数列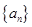 的通项公式;
的通项公式;
(Ⅱ)记 ,求证:
,求证: 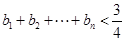 。
。
一个棱柱的直观图和三视图(主视图和俯视图是边长为 的正方形,左视图是直角边长为
的正方形,左视图是直角边长为 的等腰三角形)如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
的等腰三角形)如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.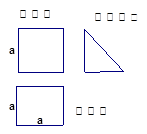
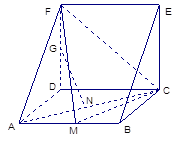
(Ⅰ)求证: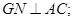
(Ⅱ)当FG=GD时,证明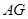 //平面FMC;
//平面FMC;
(Ⅲ)求三棱锥 的体积
的体积
(本小题满分12分)在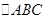 中,角A,B,C所对应的边分别为a,b,c,c=2,
中,角A,B,C所对应的边分别为a,b,c,c=2,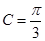 .
.
(1)若△ABC的面积等于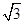 ,求a,b;
,求a,b;
(2)若 ,求b.
,求b.
(本小题满分10分)某校高二年级有男生105人,女生126人,教师42人,用分层抽样的方法从中抽取13人,进行问卷调查.设其中某项问题的选择支为“同意”,“不同意”两种,且每人都做了一种选择.下面表格中提供了被调查人答卷情况的部分信息.
| 同意 |
不同意 |
合计 |
|
| 教师 |
1 |
||
| 女生 |
4 |
||
| 男生 |
2 |
(1)请完成此统计表;
(2)试估计高二年级学生“同意”的人数;
(3)从被调查的女生中选取2人进行访谈,求选到的两名学生中,恰有一人“同意”一人“不同意”的概率.
(本小题满分13分)已知函数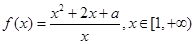
(1)若对任意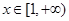 ,
,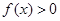 恒成立,试求实数
恒成立,试求实数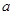 的取值范围.
的取值范围.
(2)当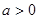 时,求函数
时,求函数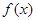 的最小值
的最小值