（本小题14分）已知函数
.
（1）若
在
上的最大值为
，求实数
的值；
（2）若对任意
，都有
恒成立，求实数
的取值范围；
（3）在（1）的条件下，设
，对任意给定的正实数，曲线
上是否存在两点
、
，使得
是以
（为坐标原点）为直角顶点的直角三角形，且此三角形斜边中点在
轴上？请说明理由。
在△ABC中，已知a=2，b=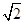
，c=
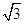+1，求A
在平面直角坐标系xOy中，曲线y=x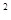
－6x+1与坐标轴的交点都在圆C上．
(Ⅰ)求圆C的方程；
(Ⅱ)试判断是否存在斜率为1的直线，使其与圆C交于A， B两点，且OA⊥OB，若存在，求出该直线方程，若不存在，请说明理由．
已知数列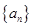
的前n项和为
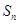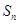，且=－n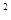
+20n，n∈N
．
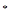(Ⅰ)求通项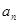
；
(Ⅱ)设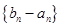
是首项为1，公比为3的等比数列，求数列
的通项公式及其前n项和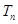
．
已知O为平面直角坐标系的原点，过点M(－2，0)的直线l与圆x
+y=1交于P、Q两点，且
(Ⅰ)求∠PDQ的大小；
(Ⅱ)求直线l的方程．
在△ABC中，角A，B，C所对的边分别为a，b，c且满足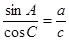
．
(Ⅰ)求角C的大小；
(Ⅱ)求
的最大值，并求取得最大值时角A的大小．