如图,已知圆锥体 的侧面积为
的侧面积为 ,底面半径
,底面半径 和
和 互相垂直,且
互相垂直,且 ,
, 是母线
是母线 的中点.
的中点.
(1)求圆锥体的体积;
(2)异面直线 与
与 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
已知射线 和点
和点 ,试在
,试在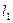 上求一点
上求一点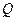 使得
使得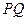 所在直线
所在直线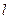 和
和 、直线
、直线 在第一象限围成的面积达到最小值,并写出此时直线
在第一象限围成的面积达到最小值,并写出此时直线 的方程。
的方程。
已知数列{an}的前n项和为Sn,且an是Sn与2的等差中项,数列{bn}中,b1=1,点P(bn,bn+1)在直线x-y+2=0上。
(1)求a1和a2的值;
(2)求数列{an},{bn}的通项an和bn;
(3)设cn=an·bn,求数列{cn}的前n项和Tn
为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图),飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤。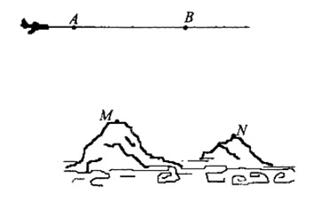
已知两直线 ,当
,当 为何值时,
为何值时, 与
与 (1)相交;(2)平行;(3)重合?
(1)相交;(2)平行;(3)重合?
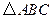 的内角
的内角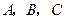 的对边分别为
的对边分别为 ,
,
且 .
.
(I)求角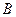 的大小;
的大小;
(II)若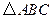 最大边的边长为
最大边的边长为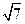 ,且
,且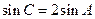 ,求最小边长.
,求最小边长.