 两地相距45千米,图中折线表示某骑车人离
两地相距45千米,图中折线表示某骑车人离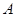 地的距离
地的距离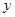 与时间
与时间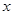 的函数关系.有一辆客车9点从
的函数关系.有一辆客车9点从 地出发,以45千米/时的速度匀速行驶,并往返于
地出发,以45千米/时的速度匀速行驶,并往返于 两地之间.(乘客上、下车停留时间忽略不计)
两地之间.(乘客上、下车停留时间忽略不计) 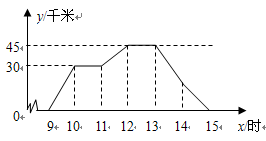
(1)从折线图可以看出,骑车人一共休息 次,共休息 小时;
(2)请在图中画出9点至15点之间客车与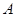 地距离
地距离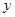 随时间
随时间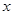 变化的函数图象;
变化的函数图象;
(3)通过计算说明,何时骑车人与客车第二次相遇.
已知二次函数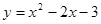 .
.(1)求出这个函数图象的对称轴和顶点坐标;
(2)求出这个函数图象与
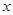 轴、y轴的交点坐标.
轴、y轴的交点坐标.
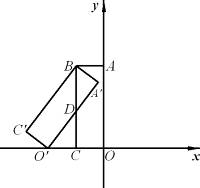
如图,矩形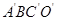 是矩形
是矩形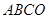 绕点B顺时针旋转得到的.其中点
绕点B顺时针旋转得到的.其中点 在
在 轴负半轴上,线段
轴负半轴上,线段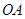 在
在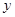 轴正半轴上,
轴正半轴上,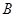 点的坐标为
点的坐标为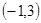 .
.
(1)如果二次函数
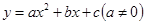 的图象经过
的图象经过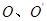 两点且图象顶点
两点且图象顶点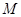 的纵坐标为
的纵坐标为 .求这个二次函数的解析式;
.求这个二次函数的解析式; (2)求边
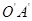 所在直线的解析式;
所在直线的解析式; (3)在(1)中求出的二次函数图象上是否存在点P,使得
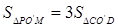 ,若存在,请求出点P的坐标,若不存在,请说明理由.
,若存在,请求出点P的坐标,若不存在,请说明理由.
.已知函数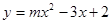 (m是常数).
(m是常数).(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若一次函数
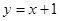 的图象与该函数的图象恰好只有一个交点,求m的值 及这个交点的坐标.
的图象与该函数的图象恰好只有一个交点,求m的值 及这个交点的坐标.
如图1,在△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕顶点C顺时针旋转30°,得到△A′B′C.联结A′A、B′B,设△ACA′和△BCB′的面积分别为S△ACA′ 和S△BCB′.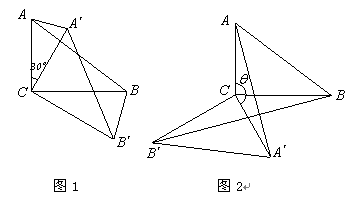
(1)直接写出S△ACA′ ︰S△BCB′ 的值;
(2)如图2,当旋转角为
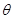 (0°<
(0°<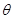 <180°)时,S△ACA′ 与S△BCB′ 的比值是否发生变化,若不变请证明;若改变,写出变化后的比值(可用含
<180°)时,S△ACA′ 与S△BCB′ 的比值是否发生变化,若不变请证明;若改变,写出变化后的比值(可用含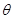 的代数式表示).
的代数式表示).
如图,在三角形ABC中,以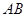 为直径作⊙O,交AC于点E,OD⊥AC于D,∠AOD=∠C.
为直径作⊙O,交AC于点E,OD⊥AC于D,∠AOD=∠C.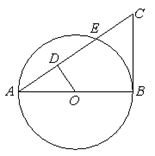
(1)求证:BC为⊙O的切线;
(2)若
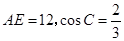 ,求OD的长.
,求OD的长.